最近，数学界有一条新闻引起了公众的关注：ABC猜想再起波澜。具体地说，日本数学家望月新一（Shinichi Mochizuki）宣称证明了ABC猜想的论文被接收了。但奇妙的是，大部分数学家并不认为这真正解决了问题。 

望月新一（见他在京都大学的主页http://www.kurims.kyoto-u.ac.jp/~motizuki/）

ABC猜想是什么？

这个猜想的名字特别简单，所以许多外行都早有耳闻。这是一个简单但非常强大的猜想，在数学中的重要性仅次于最大的难题黎曼猜想，比普通人熟悉的难题哥德巴赫猜想和孪生质数猜想还要重要。 

黎曼

ABC猜想的重要性在于，如果它是正确的，那么就建立了加法和乘法之间的某种联系。哥德巴赫猜想和孪生质数猜想之所以迷人和困难，也都是因为它们涉及了加法和乘法之间的关系。在这两种基本的运算之间建立起联系，影响将是非常深远的。

如果证明了ABC猜想，那么立刻可以推出很多重要的结论。例如费马大定理，就是费马说“我想到了一个绝妙的证明，但页边太窄我写不下”的那个。 

费马大定理

费马大定理折腾了人类300多年，直到1995年才由英国数学家安德鲁·怀尔斯（Andrew Wiles）证明，这个证明长达几百页。 

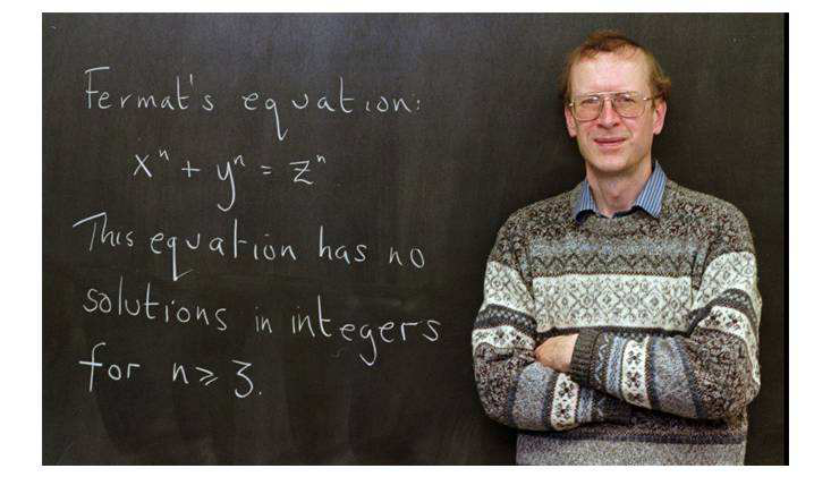
安德鲁·怀尔斯

而假如ABC猜想成立，那么我们用几行就能证明费马大定理。对ABC猜想的威力有些概念了吧？ 

用ABC猜想证明费马大定理（https://www.sohu.com/a/212354205_100082182）

如果你想了解ABC猜想具体是什么意思，以及上面这个简短的证明是怎么推理的，我们会在后面的附录中详细解释。在这里可以简单地解释，ABC猜想说的是：

如果有两个互质的自然数a和b，它们的和a + b = c，那么在绝大多数情况下，abc的根积rad(abc) > c。

如果你对“互质”和“根积”这两个概念不感兴趣，那么可以跳过后面的数学讨论。如果你想知道它们是啥意思，下面这个简短的解释就足够。

每一个自然数都可以分解质因数，即写成若干个质数的乘积。例如

10 = 2 × 5，

12 = 2² × 3，

27 = 3³。

这里面可能每个质因数只出现一次，例如10，也可能有些质因数出现多次，例如12和27。

两个自然数如果没有共同的质因数，也就是说最大公约数等于1，那么我们就说它们是互质的（coprime）。例如10和27互质，而10和12

互质。请注意，互质并不意味着这两个数本身是质数。它们俩都可以是合数，仅仅是没有共同的质因数而已。

如果a和b互质，c = a + b，那么c跟a、c跟b也互质。为什么呢？假如不是这样，比如说c跟a

互质，那么它们都可以被某个质因数k整除。但b = c - a，所以b也可以被k整除。这样a和b就

互质了，跟前提矛盾。因此，c必然跟a和b都互质。所以，我们可以把ABC猜想讨论的(a, b, c)这三个数称为一个互质三元数组。

互质是一个小学数学里就有的概念，而根积（radical）就稍微高深一点。它的定义是，一个自然数的所有质因数相乘一次，无论这个质因数出现多少次。例如10的根积就是

2 × 5 = 10，

12的根积就是

2 × 3 = 6，

27的根积就是3。

一个有趣的问题是，1怎么办？1既不是质数也不是合数，我们定义它的根积等于1。

根积的英文是radical，一个数a的根积写成rad(a)。显然，rad(a)总是小于等于a，只有在a的每个质因数都只出现一次时才取等号。

ABC猜想关心的问题就是：abc三个数乘积的根积即rad(abc)，跟c相比，哪个大？

它猜测的答案是：在绝大多数情况下，rad(abc) > c。

做一些数值实验，就能对此有些概念。

例如：a = 2，b = 7，c = 9 = 3²。这时rad(abc) = 2 × 7 × 3 = 42 > c。

又如：a = 1，b = 8 = 2³，c = 9 = 3²。这时rad(abc) = 1 × 2 × 3 = 6 < c。

又如：在固定c = 81 = 3⁴的情况下，在a和b的所有组合中，只有两种情况满足rad(abc) < c，分别是1 + 80 = 81和32 + 49 = 81，其他的全都是rad(abc) > c。大家可以验证这一点，然后想想，这是为什么。

通过这些数值实验，很快就可以理解，对于一般的互质三元数组(a, b, c)，rad(abc) > c是通例，rad(abc) < c是反例。不过，这只是对ABC猜想的一个粗略描述，因为所谓“绝大多数情况”是个不严格的表述，是给外行听的。数学家有一套精确的语言，来描述“绝大多数情况”是什么意思。

反例有多少个呢？假如反例只有有限多个，那么它相对于无限多的通例自然是少得多。但其实我们可以证明，反例是无限多的，所以ABC猜想并没有这么简单。但数学家有一套语言来描述，这无限多的反例仍然是极其少见的。

对于非专业人士来说，了解这么多已经相当不错了。你现在就可以去跟外行对线，说你是ABC猜想的专家。如果你想搞清楚反例为什么有无限多以及如何严格表述ABC猜想，那么请参见后面的附录，欢迎大家更上一层楼。

下面的问题是，ABC猜想引起了什么争议呢？

ABC猜想是在1985年，由法国数学家乔瑟夫·奥斯达利（Joseph Oesterlé）和英国数学家大卫·马瑟（David Masser）提出的。 

乔瑟夫·奥斯达利 

大卫·马瑟

2007年，法国数学家吕西安·施皮罗（Lucien Szpiro）提出了一个证明，但很快被发现有错误。2012年，日本数学家望月新一提出了一个证明，然后有趣的事情发生了。

最大的有趣之处在于，别人听不懂他在说什么。

新一君自创了一套理论，称为“宇宙际Teichmüller理论”。这名字乍一看吓人一跟头，不过搜索一下就会发现Teichmüller是一位德国数学家的名字，早就有Teichmüller理论、Teichmüller空间之类的术语了。 

宇宙际Teichmüller理论（见望月新一的论文页面http://www.kurims.kyoto-u.ac.jp/~motizuki/papers-japanese.html）

新一增加的，是那个前缀“宇宙际”。这个词乍一看好似奥特曼风格，不过看一下英文就明白是inter-universal。虽然还是不知道具体意思，不过inter和universal都是数学里的常用词，这就好理解多了。

雪上加霜的是，新一自创了很多术语和符号。例如“霍奇剧院”（Hodge theatre），这个概念的定义如下。 

霍奇剧院的定义

如果说有一种美德叫做“用户友好”，那么新一显然对此完全没有考虑！

他的特立独行还表现在，这些论文并没有发在学术期刊上，也没有发在预印本平台上，而是发在自己的主页上。我的地盘我做主，独立特行到如此程度的科学家现在实在太少见了！

一般而言，当你提出了一个长篇的证明时，你应该四处去做讲座，向同行解释你的想法。怀尔斯就这样做过。证明庞加莱猜想的俄罗斯数学家佩雷尔曼（Grigory Perelman）是个非常愤世嫉俗的人，但他也这样做过。偏偏新一就不干，别人请他去讲他也不去。 

佩雷尔曼

有些数学家认真研究了新一的论文，然后指出了一些错误。新一做了相应的修正，宣称这些错误已经补上了。

但是，两位德国数学家舒尔茨（Peter Scholze）和斯蒂克斯（Jakob Stix）认为，论文中有些地方的错误是不可弥补的。舒尔茨是数学界最高奖之一菲尔兹奖的得主，所以这个批评是十分严重的。在大多数数学家看来，就不值得花大力气去研究新一的论文了。然而新一认为，是他们错误理解了自己的证明，论文不需要做任何修改。双方为此闹翻了，这个争论到现在都没解决。 

舒尔茨 

斯蒂克斯

舒尔茨和斯蒂克斯的文章《为什么ABC仍然是猜想》

最近的新进展是，2020年4月3日，有一个数学杂志宣布接收了新一的论文。但令人挠头的是，这个杂志的主办单位就是新一所在的京都大学数理解析研究所，而且主编就是他自己。这样做，真的没有瓜田李下之嫌吗？

不过我们立刻要补充一下：按照杂志的描述，新一并没有参与审稿。他甚至连新闻发布会都没参加。在这些方面，还是有节操的。说到底，数学界怀疑的还是论文本身的问题。论文被接收，并没有改变大多数数学家的看法，——信的照样信，不信的照样不信。 

专业论坛上的讨论认为，望月新一的论文被接收没有改变大多数数学家的负面看法（https://www.math.columbia.edu/~woit/wordpress/?p=11709）

如果你问我，望月新一的证明对不对？我当然不知道，这是超级内行才有资格判断的事。不过，基于科学研究的普遍经验，我很赞同华人菲尔兹奖得主陶哲轩的评论。 

陶哲轩

他的基本意思是，一个好的想法应该有很多用处，而不是只能干一件事。像张益唐和佩雷尔曼的工作，从一个新思路出发，很快就得到了一些有趣的结果，令人信心大增。而望月新一的理论却不是这样，推了300多页，只是为了ABC猜想这一件事。你觉得这是奇迹呢，还是错误呢？恐怕是错误的可能性更大。 

张益唐

【陶哲轩的原文是英文，下面有一个中文翻译】（https://www.sohu.com/a/214344881_199523）：

 “我没有足够的知识对望月的论文做专业的评价，但对您所提到的张益唐和佩雷尔曼的工作非常熟悉。它们之间一个显著的区别在于张益唐和佩雷尔曼在论文的开始就给出简洁的‘概念验证’，而他们所发展的方法也能很快地用于相应领域，得到一些有意思的非平凡新结果，或是给出一些已有的非平凡结论的新证明。望月的论文缺乏这样的‘概念验证’。

在佩雷尔曼的论文中，第5页就已经给出了Ricci流的全新解释：它将Ricci流视为梯度流，看起来非常有潜力。在第7页，他就用该解释建立了一个关于Ricci流的精彩定理。虽然这个定理相距最终证明庞加莱猜想甚远，但它本身就是一个新奇而有趣的结果，使得这个领域的专家迅速认定这篇论文有很多‘好东西’。

张益唐的54页论文沿袭了解析数论的传统，将所要用到的引理放在论文的开头，因此有不少对专家而言是标准性的内容。但是这些引理陈列之后的第6页，张益唐就给出了一个非平凡的观察：只要能改进Bombieri-Vinogradov定理对光滑模的估计，就能证明素数间距离有限。这并非这篇论文最深刻的部分，但是它将原问题简化为更容易处理的问题。与此相反，无数试图攻克像黎曼猜想这样大问题的论文不断将原有问题复杂化，直到奇迹发生，而这样的奇迹通常只是一个错误。

从我了解的信息来看，望月工作的‘概念验证’就要300多页，这样才能证明ABC猜想。在我看来，如果能有一个更简短的，比如少于100页的 ‘概念验证’，就有可能帮助人们消除对这一证明的疑问。如果需要300多页来建立一个全新的独立体系，而这个体系只能用来证明ABC猜想，却没有任何其他的外在意义，这将是一件非常奇怪的事情。”

最后，欢迎大家关注我们的账号“科技袁人”。我想，这个普遍的道理对观众朋友们来说，是比ABC猜想本身更大的收获。

附录：ABC猜想的严格表述

我们在前面说到，ABC猜想的内容是：两个互质的自然数a + b = c，那么abc三个数相乘的根积rad(abc)在绝大多数情况下大于c，只在极少数情况下小于c。

我们来仔细想想：rad(abc)跟c相比哪个大，是由什么决定的？

稍微思考就会发现，答案取决于在这三个数的质因数中，有多少个是出现多次的。

如果c的所有质因数都只出现一次，那么rad(c) = c。再乘上a和b的质因数，rad(abc)肯定就大于c了。

如果c有些质因数出现了多次，那么rad(c) < c。所以问题就是：乘上a和b的质因数，是否足以补偿从c到rad(c)的损失，把rad(abc)拉到大于c呢？

由此我们可以理解，反例的特点是，在a、b、c中包含质因数的高次幂。这样才能把rad(abc)拉得尽量低，以至于低于c。

例如前面举的1 + 80 = 81，这时b = 80 = 2⁴ × 5，c = 81 = 3⁴，

rad(abc) = 2 × 5 × 3 = 30 < c。

又如32 + 49 = 81，这时a = 32 = 2⁵，b = 49 = 7²，c = 81 = 3⁴，

rad(abc) = 7 × 2 × 3 = 42 < c。

现在我们在直觉上可以理解，rad(abc) > c的通例是绝大多数，rad(abc) < c的反例是极少数。但真正的问题在于，什么叫做绝大多数和极少数呢？

如果反例只有有限多个，那么相对于无穷多组（a, b, c），当然就是极少数了。但我们立刻可以证明，反例有无限多个。

例如，令

a = 1，

b = 2⁶ⁿ - 1，

c = 2⁶ⁿ，

其中n是自然数。

这时c的质因子只有一个2，所以

rad(abc) = 2 rad(b)。

下面我们来考虑一下，b有哪些质因子？

注意到

b = 2⁶ⁿ - 1= 64ⁿ - 1 = (63 +1)ⁿ - 1，

用二项式定理展开，立刻发现它可以被63整除。

63 = 9 × 7 = 3² × 7，

所以b的质因子中至少出现了两次3，因此

rad(b) ≤ b/3。

由此可见，

rad(abc) = 2 rad(b) ≤ (2/3) b < b < c。

这对任何自然数n都成立，所以这样的反例有无穷多个。

所以，我们该怎么描述这个无穷多的极少数呢？

用微积分里常用的思路，我们可以说：虽然rad(abc) < c的反例有无穷多个，但如果在那个较小的量上加一个指数，把它变大一点，那么无论这个指数多么小，反例就都只有有限多个了。

用数学语言表述，就是：对于任意的正数ε，满足

rad(abc) ^1 + ε < c 

的互质三元数组（a, b, c）都只有有限多个。

这就是ABC猜想的一种常用表述。

另一种等价的常用表述是，先定义一个量叫做互质三元数组（a, b, c）的“品质”（quality），

q(a, b, c) = lnc / ln[rad(abc)]。

显然，q < 1就对应通例，q > 1就对应反例。

那么，q > 1的那些反例有什么特点呢？

上面的第一种表述等价于说，大于1的q虽然有无穷多个，但对于任意一个正数ε，大于1 + ε的q都只有有限多个。这就是ABC猜想的另一种常用表述。

这是一个非常有意思的分布。大于1的q虽然有无限多个，但你如果问：大于1.1的q有多少个？回答是只有有限个。

再问：大于1.01的q有多少个？还是只有有限个。

即使你问：大于1.0000001的q有多少个？还是只有有限个。

由此可见，在1到任意小的1 + ε之间，都包含了几乎全部的大于1的q。在外面的漏网之鱼总是可以数出来，而不是无限多。

由此还可以推出，在所有的q值中存在一个最大值。如果不是这样的话，大于1 + ε的q就有无限多个了。

那么，这个最大的q值是多少呢？目前还不知道。不过通过数值搜索，已知的最大q值出现在下面这个三元组中：

a = 2，

b = 3¹⁰ × 109 = 6436341，

c = 23⁵ = 6436343。

它的rad(abc) = 2 × 3 × 109 × 23 = 15042，

你看，它比c小得多。这个三元组的

q = ln6436343 / ln15042 = 15.677 / 9.6186 = 1.6299。

有一个分布式计算项目，叫做ABC@home（http://www.equn.com/wiki/ABC@home ）。它的目标是，利用大家空闲的计算资源，穷举算出直到 c ≤ 1018 的反例三元组。这样虽然不能证明ABC猜想，但通过观察反例的分布，也许能够提供一些洞察。 

ABC@home的研究内容简介

下面，我们来看如何通过ABC猜想证明费马大定理。费马大定理说的是：

对于任何大于2的自然数n，xⁿ + yⁿ = zⁿ都没有正整数解。把xⁿ、yⁿ和zⁿ理解成a、b和c，就很容易看出它和ABC猜想之间的联系。

用ABC猜想证明费马大定理（https://www.sohu.com/a/212354205_100082182）

在前面的ABC猜想的第二种表述中，假定我们已经知道q的最大值不超过2，也就是说，任何的互质三元数值都满足c < rad(abc)²，没有反例。这并不完全等价于ABC猜想，而是一个跟它有密切联系的猜想。

假如a = xⁿ，b = yⁿ，c = zⁿ，那么根据根积的定义可知，

rad(abc) = rad[(xyz)ⁿ] = rad(xyz) ≤ xyz < z³。

在这里用上c < rad(abc)²，就得到

c = zⁿ < rad(abc)² < z⁶。

这说明，费马大定理如果不成立，那么n必然小于6，也就是只能取3、4、5。但欧拉已经证明了n = 3的情况，费马自己证明了n = 4的情况，狄利克雷和勒让德证明了n = 5的情况，所以这些可能都排除了。 

欧拉

费马

狄利克雷

勒让德

结论就是：费马大定理对所有的n都成立。

你看，这就是ABC猜想小试牛刀。如果它真的被证明成立，必将带来一场革命！

责任编辑：计欣晔

文章来源：风云之声微信公众号