本次内容来自系列视频课程

 “一说万物：现代物理学百年漫谈”

第六讲：复杂

6.3海岸线是无穷长的吗？

（视频链接：https://v.qq.com/x/page/x3138dkzozi.html）

话说有一个青年，他感觉人生苦闷，便去找一位禅师。青年问：“为什么我的人生如此曲折呢？”禅师说：“青年人，一段曲折的曲线，你把它放大了不就是直线了吗？”青年人默默地拿出一段英国的海岸线。

当然，这是一个段子，我们来考虑一个不太段子的版本。青年人非常苦闷，因为他搞不清楚英国的海岸线有多长，他跑去问禅师：“禅师，英国的海岸线有多长？”禅师翻了他一眼，说：“青年人，你是不是对英国的海岸线存在偏见呢？”

如果你是那位青年的话，你是不是感觉找错人了？你是不是感觉这个禅师其实是一个喷子？但其实这个禅师说的是对的，确实，青年提出这个问题是因为他对英国的海岸线真的存在偏见。因为英国的海岸线是一个自相似的结构，不光是英国，所有海岸线都是自相似的结构：如果我们考虑海岸线当中的一段，并将其放大，放大以后看起来和原来的海岸线非常像，你再取一段去放大，放大之后又和原先的海洋线非常像，这就是自相似结构，人们给它取了一个名字——分形结构。 

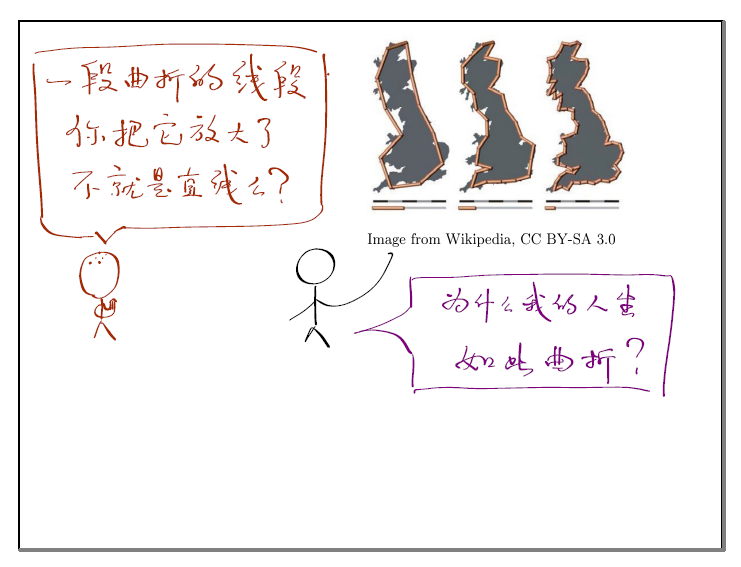
英国海岸线是随机的自相似，比较难以研究，为了研究分形结构，现在我们考虑一个简单的自相似结构，叫做“希尔伯特曲线”。什么叫希尔伯特曲线？首先，由下图中①开始，非常简单的三段式曲线；然后把其中的每一段即每一个基本单元一分为二，用自相似的结构去取代，当然用自相似的结构取代之后，它不连续了，中间有了一些没有连上的地方，我们人为的连上；不断重复以上操作，进行无穷多次，所得到的曲线就叫做希尔伯特曲线。

希尔伯特曲线有什么样的性质？这个曲线是一个充满空间的曲线，也就是说，可以证明，方框内的任何一点实际上都在希尔伯特曲线上。 

现在问题来了，希尔伯特曲线是几维的曲线？你可能说它是一维的，它是一条线嘛，线就是一维的；或者说，你可以用一个参数表示它。但是，你也可以从另一个角度看，它把方块里的每一点都充满了，它应该是一个二维的图形：方块是二维的图形，方块中的每一点组成的集合应该也是二维的图形。

可见，这个曲线暴露了我们脑海里对空间图形维数的一些偏见。这个曲线到底是几维的呢？这取决于你如何定义一个图形的维数。

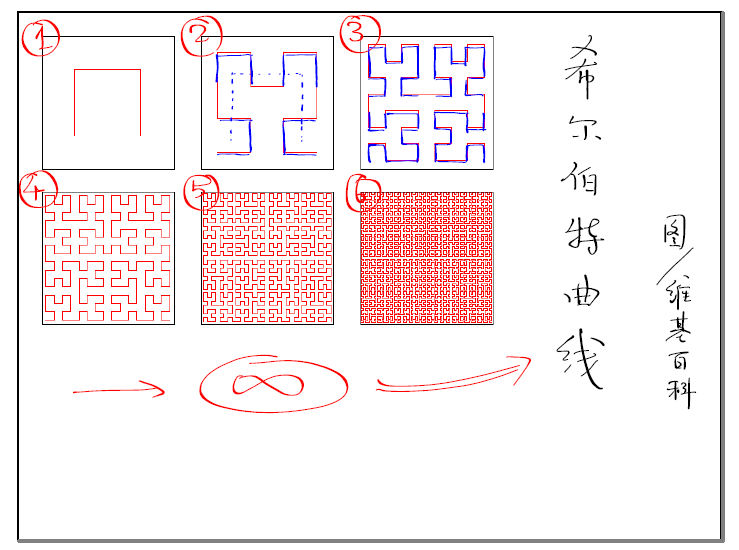
有一种定义方式叫做豪斯多夫维数。如果图形有基本的单元，那么当你把每一个基本单元一分为二，这个图形变成了几个自相似的结构呢？比如说一条线，你把基本单元一分为二，它变成了两个自相似的结构，它是一维的；一个方块，你把每一个基本单元都断开的话，它变成了4个自相似结构，即2的2次方，它是二维的。希尔伯特曲线看起来是不是非常像方块的自相似行为，所以说希尔伯特曲线应该是二维的。

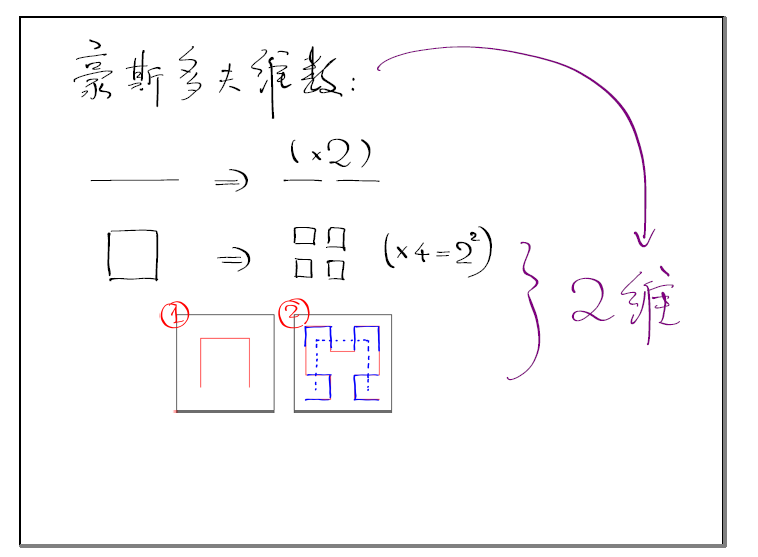
这只是形象的比喻，实际上，豪斯多夫维数在数学上可以被严格定义。你把每一个基本元素分成了几段，然后你这个图形变成了多少个自相似的元素，自相似元素的个数取对数除以分成的段数取对数，得到的结果就是几何图形的维数即豪斯多夫维数。

这里你要问了，你怎么保证维数是整数？谁告诉你维数必须是整数的，不一定，维数也有可能是个小数。比如，我们考虑这样一个例子——科赫雪花。

首先，有一段直线段，然后把线段中间挖掉一块，也就是说，把基本单元一分为三；一分为三之后，给中间位置添加一个“包”。这样会变成什么呢？中间鼓个“包”以后，基本单元一分为三了，但是在其中插入了4个自相似的结构。以此类推，一直迭代无穷多次，就得到了“科赫雪花”。这种奇奇怪怪的形状，叫做分形，所以豪斯多夫维数也经常被叫做分形维数。

那么，科赫雪花的分形维数是多少呢？在计算之前，你可以想一想，这个东西基本上是一条线，对不对？所以它的分形维数应该跟1差不多。但是它里边鼓了包，大包套小包，所以它的分形维数应该比1多一点。 

好，我们算一下。把每一个基本单元一分为三，结果得到了4个自相似的部分，也就是说，分形维数是log 4除以log 3，大约是1.26，比1要多一点。前面讲的希尔伯特曲线，它的分形维数是2。 

下面回到长度的问题，你问“希尔伯特曲线它有多长”，希尔伯特曲线的分形维数是二维，二维的一个图形，你问它有多长，你是不是对它有偏见呢？希尔伯特曲线也好，科赫雪花也罢，你是不能问它的长度的。同样，海岸线你也不能问它的长度，当你问海岸线有多长时，你是对这个海岸线有着偏见。当你用直尺去量的时候，会发现尺越短量出来的海岸线则越长，最后越量越长，直至无穷长。这个无穷长的荒谬结果，就是你对海岸线有偏见的代价。

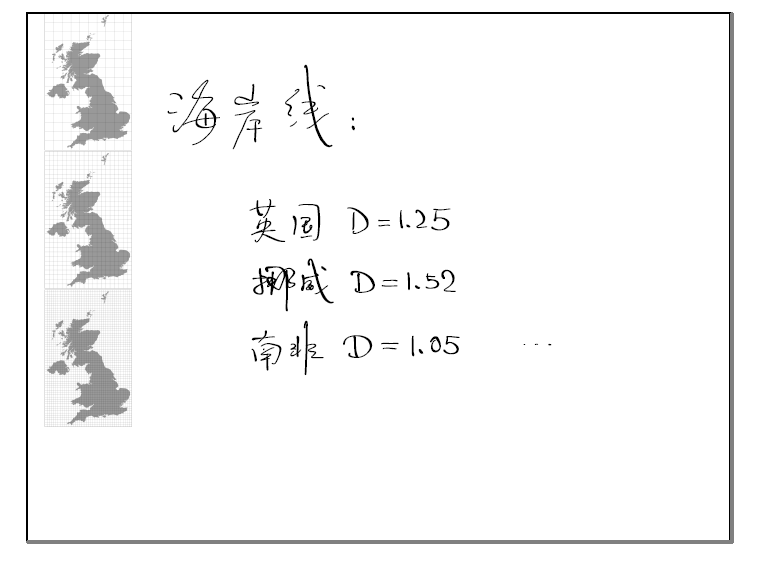
不同地方海岸线的长度都是无穷长，但是它们的分形维数是不一样的。英国海岸线的分形维度是1.25，挪威是1.52，南非是1.05。看起来越曲折复杂的海岸线，其分形维度就越高。

那么，人是几维的生物呢？ 

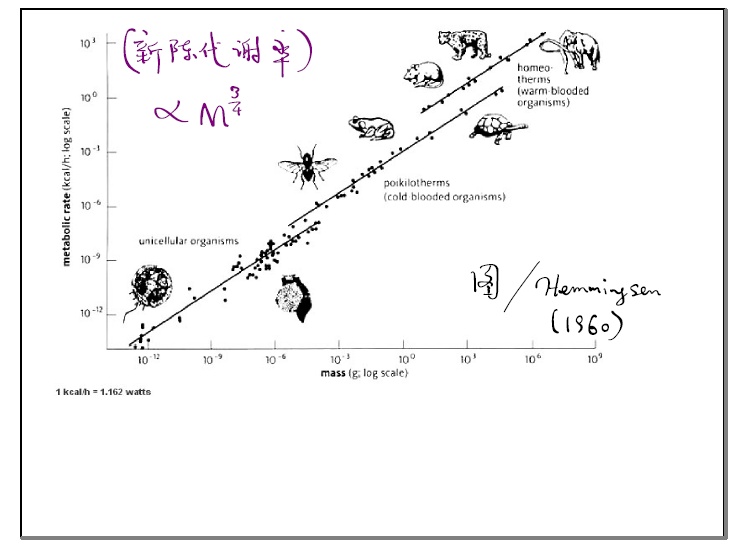
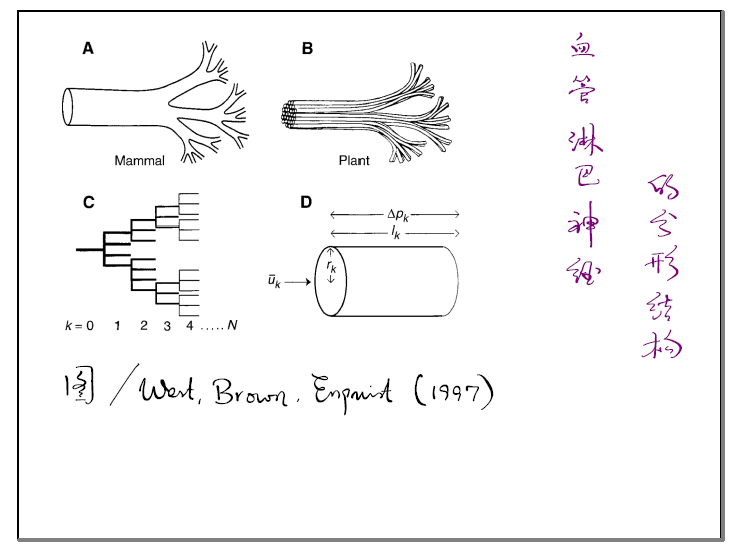
从豪斯多夫维数上讲，其实人并不是三维的生物，你谈论它的体积也是对人存在一定的偏见。你想，人是多么复杂，人的血管、人的神经、人的淋巴等等摆放在一个有限的体积内。1960年代，人们发现了一个很奇怪的现象。我们分析不同动物，从小动物到大动物，不同动物的新陈代谢率服从什么样的规律呢？如果你没有仔细想，第一感觉可能会认为新陈代谢率应该正比于细胞的数量。但是人们发现，新陈代谢率却是和质量的3/4次方大概成正比的。这件事很奇怪，出来了两个简单整数4和3的比例。这两个数是怎么出来的呢？你可能已经猜到了，这个3是空间的三维，这个4是人类的分形维数是4。

人虽然在三维空间当中，但是某种意义上说，我们是生活在四维中。

（责任编辑：杨玉露）

（版权说明，转载自：墨子沙龙公众号）