
本次内容来自系列视频课程
“一说万物:现代物理学百年漫谈”
第七讲:狭义相对论
7.1钟变慢,尺缩短

(视频链接:https://v.qq.com/x/page/j31432hykpu.html)
今天,我们开始进入相对论的世界。相对论基于两条基本假设,相对性原理和光速不变原理。
相对性原理告诉我们,如果你在一个平稳的车厢里而不往外看,那么即使车在作匀速直线运动,你也感受不到车的运动。也就是说,运动是相对的,没有绝对运动,或者说惯性系中物理定律的形式是不随你选哪一个惯性系而变化的。这就是相对性原理。
光速不变原理,顾名思义是指:在真空中,光的速率是不变的。首先,需要在真空中,如果在介质中的话,光速有可能有变化;其次,速率不变而不是速度不变,即速度的大小是不变的。
这就是狭义相对论的两个基本假设。其实狭义相对论里还隐藏着另一基本假设,只不过它太简单了,以至于我们认为根本没必要把它特意指出来,即:关于在空间中的一个点、时间上的一个时刻发生的事件,这个事件的发生与否是不依赖于不同的观测者而变化的,也就是侦探小说里经常说的——真相只有一个。
相对性原理、光速不变、真相只有一个,这三个基本假设支撑起狭义相对论。下面我们就来看一看,相对论里蕴含着什么神奇的现象。

我们想问的第一个问题是时间。牛顿说时间是绝对的,爱因斯坦就问:绝对的时间到底对不对呢?
在《自然哲学的数学原理》中,牛顿说:“Absolute, true and mathematical time of itself, and from its own nature, flows equally without regard to anything external, and by another name is called duration.”意思是,时间是绝对的、真实的和数学的,它自己流淌,和任何其他事物没有关系,那么它叫做“间隔”。

我引用牛顿的话并不是去嘲笑牛顿,说牛顿有多么不对,相反,你想一想,在牛顿的时候,他居然会去想这个问题。虽然鉴于时代的约束,他最后没有给出一个正确的答案,但是他居然会去想这个问题!并且他又说:“relative, apparent and common time is some sensible and external measure of duration by means of motion.”即:我们通常所说的时间是通过运动去对绝对时间的一种相对的测量。
被现代观念所武装起来的我们可能就觉得有点不对了,因为牛顿说绝对时间是可以被探测的,但又不能被影响。大家想一想,这个世界上存不存在任何的可以被探测又不能被影响的东西?恐怕想不出任何一个例子。牛顿自己就讲,作用力等于反作用力,有作用力必然有反作用力,有探测必然会有一个影响的反作用。我们又有量子理论里的不确定性原理,它告诉我们,测量一个系统往往会对这个系统产生影响。牛顿的绝对时间为什么能这么卓尔不群、特立独行,可以被探测又不能被影响呢?

其实这个概念是有问题的。当然我们绕来绕去,还都是在哲学的范畴内坐而论道,如果想在物理学的范畴内质疑牛顿的绝对时间,我们需要构想一个可以进行实际测量的方法。
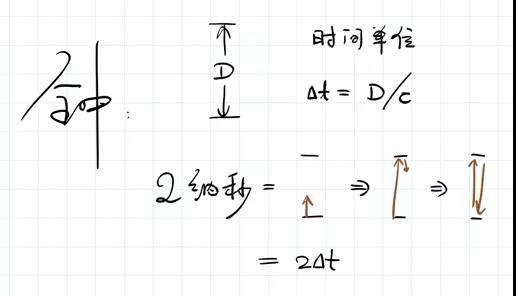
怎么办?我们希望能用一个操作足够简单又方便我们想清楚的办法定义什么是时间。好,下面我们来定义一个钟,最简单的钟,叫光钟。假设有这样的一条线段,线段的长度是D,在线段底部装有一个发射器,可以把光发射上去,发射到上面以后,上面有一面镜子,再把光反射回来。我们把这样的装置叫光钟。对于这个光钟,从下到上的时间Δt = D/c,这里c是光速。我们可以规定时间单位(比如1纳秒)就是光从下到上的时间。这就是我们定义的光钟。

现在我们利用光钟去研究时间的相对性。为了研究时间,我们引入两个人物张三和赵四。
第一步,定义时间Δt = D/c。我们通过上述光钟来完成。
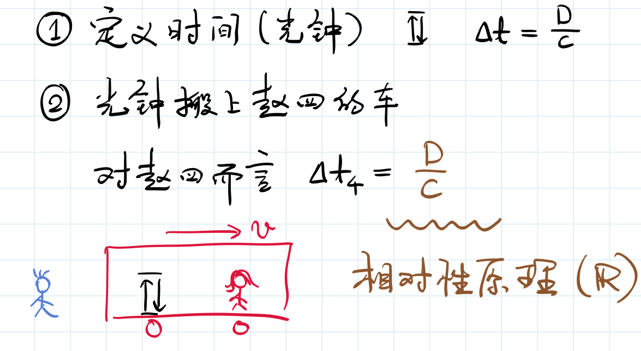
第二步,把光钟搬上赵四的车。赵四在车上,车匀速直线运动,在这个情况下,对于赵四而言,他的时间Δt4就是光钟的光从下边发出来,然后到顶上镜子。(Δt4中,这个4代表的就是赵四,角标3则代表张三。)对于赵四而言,Δt4应该也是D/c,即原来那个Δt,因为相对性原理要求如此:赵四在车里,他不往外看的话,他不知道这个车在运动,所以说花的时间应该和光钟没有放到车里的时候花的时间一样多。
第三步,现在我们来看,对于张三而言,光钟从下到上,然后再从上到下,这样一个循环要花多少时间呢?这是问题的关键。你可能会问一个问题:对于张三而言,光钟的高度还是D吗?怀疑一切的精神是非常可嘉的,但其实光钟的高度还是D,也就是说,垂直于运动方向的线段的长度是不变的。为什么?我们用反证法。假如垂直于运动方向的长度会改变,那么我们想一个例子,比如火车在铁轨上跑,假如垂直于运动方向的长度会变短的话,在火车上看,铁轨间距变短了,车轮就跑到铁轨外边去了。而如果在铁轨看的话,垂直于运动方向,火车轮子之间的距离变短了,轮子就跑到铁轨的里边去了。但真相只有一个,火车上的人认为铁轨跑到里边去了,铁轨上的人认为轮子跑到里边去了,这就不对了,所以说垂直于运动方向的线段长度应该是不变的。
好,对于张三而言,光钟从下边跑到上边的时间间隔Δt3变成什么了?为了解释这个问题,首先我们注意到一点:光钟的光会打到上边镜子这个物理事件是不变的。所以,光线现在必须斜着跑了。首先光发射出来,过了Δt3的时间,光钟跑了车速v乘以Δt3,光跑了cΔt3。我们下面要解的就是一个简单的勾股定理问题了,希望大家暂停一下,自己进行求解。
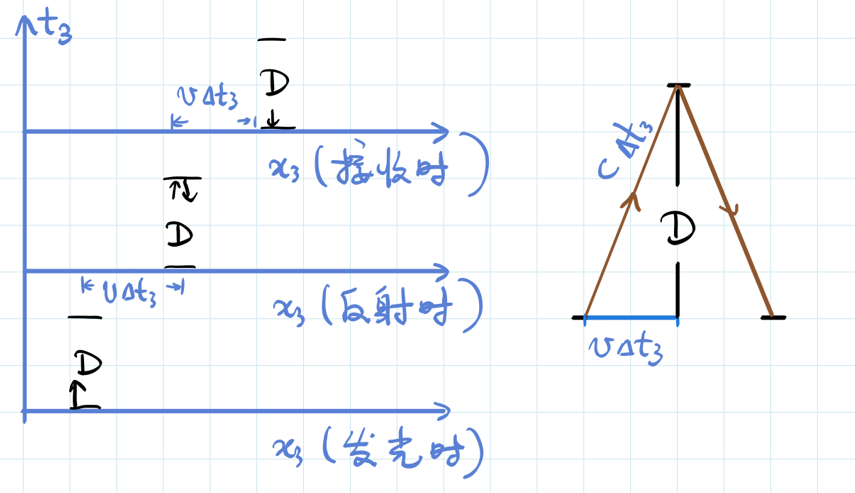
求解发现,Δt3等于一个根号算式乘以D/c,见下图。而D/c就是赵四的时间间隔Δt4。而前边这个根号,我们给它设成一个量叫γ。看,γ是大于等于1的,如果车速 v不等于0,那么γ一直是大于1的一个数。也就是说,在张三看来,赵四的光钟变慢了。
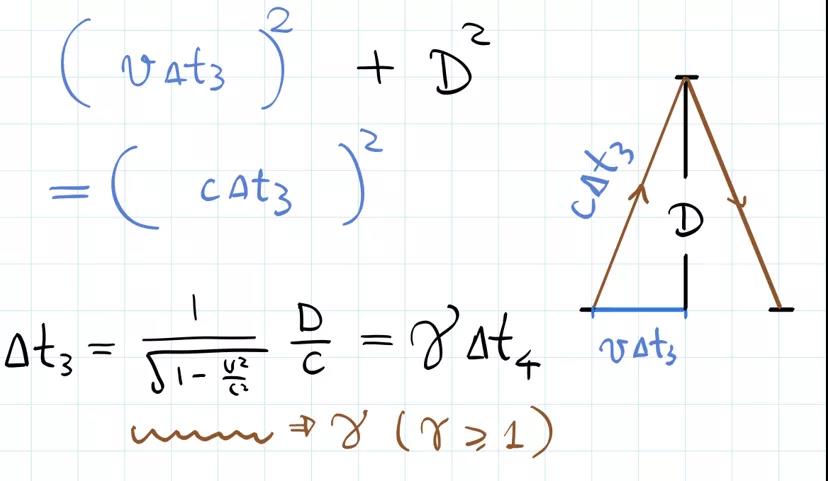
说到这儿,你有可能不服。你定义了一个光钟,但是谁说这个光钟说的就算呢?有可能有别的钟,这个光钟变慢了的话,那么别的钟是变慢了还是不变呢?别的钟也必须和光钟一起变慢。为什么这么讲?如果车外的张三看见光钟变慢了,而别的钟没变慢。光钟变慢,别的钟没变慢,这是一个事实。这个事实不光张三要同意,赵四也要同意,对不对?也就是说,赵四在车上,他没往外边看,平白无故的当车运动的时候,光钟走的速度就和别的钟不一样了,这可能吗?不可能,因为违背相对性原理。
相对性原理告诉我们,不仅是光钟,一切的钟,任何你能想象到的钟——不光是你从商店买的钟,还有手机上显示的时间,还有你测脉搏显示出来的时间,甚至人变老的速度,心跳的速度,一切的钟在运动的时候,在外边的观测者看来,它都变慢了。

这里我强调一下,不是自己看来,自己看来一切如常,而是在外面的观测者看来,运动者携带的所有的钟都变慢了。时间并不是绝对的,时间是相对的。

下面我们做一个小练习。假如有一个手雷,如果我不扔出去的话,我把弦一拉,它需要Δt的时间爆炸。好,现在我把弦一拉,马上以非常快的速度v扔出去,那么手雷能跑多远?

在我(即外边不动的观测者)看来,运动的手雷的时间变慢了,它的速度是v,它的时间是γ乘以Δt,所以手雷可以跑的距离是γvΔt。特别地,如果我把手雷扔得特别快,速度接近光速的话,这个手雷可以跑近乎无穷远。越接近光速,手雷跑得越远,趋向于无穷远,这是相对论给我们非常不一样的一个效应。
我们换位思考,不从我自己的角度,而从手雷的角度想一想,会出现什么样的事情?从地面观测者看来,这个手雷是延年益寿了,但是从手雷自己的角度,它看自己的时间没有变慢。它自己没有觉得时间变慢,但是它怎么跑得更远了呢?这就涉及相对论里的另外一个效应,叫尺缩效应。
在手雷看来,大地是在运动的,对不对?大地运动的时候,大地是会缩短的,大地缩短的因子也是γ这样的一个因子。手雷自己看自己没有“延年益寿”,但是它看到大地“缩地成寸”了。也就是说,我们不仅能看到运动的钟变慢,也能看到运动的尺缩短。

(责任编辑:杨玉露)
(版权说明,转载自:墨子沙龙公众号)
