本次内容来自系列视频课程

“一说万物：现代物理学百年漫谈”

第七讲：狭义相对论

7.2天涯共此时吗？

（视频链接：https://v.qq.com/x/page/a3146wpb52i.html）

上一节讲了时间和空间的相对性，今天我们来看一看相对论的时空观，即在狭义相对论里，我们如何建立时间和空间。

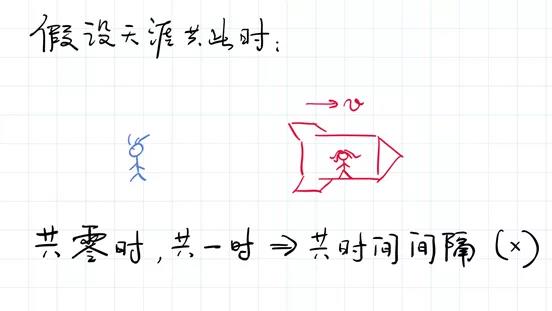
唐代诗人张九龄写过这样一句诗：“海上生明月，天涯共此时”。天涯共此时的现象，在相对论里是一定会发生的吗？假设天涯一直共此时，那么张三和李四共了零时、共了一时，也就是说他们共了一个小时。而如果张三和李四一个静止、一个匀速直线运动，他们认为一小时的时间间隔是同样的时间，这就不对了。因为我们知道，时间间隔是相对的，赵四运动的时候，张三看到赵四的时间间隔变长了。所以说，“天涯共此时”这句话肯定在什么地方有问题？什么地方有问题呢？

首先我们想一想，这句话对于同一个地点的情况会不会有问题？在同一个地点不会有问题的，为什么？我们做一个理想实验，假如说张三犯了法，做了一件人神共愤的事情，然后从天上“咔、咔”打下来两个大雷，这两个大雷同时打在张三的头顶上。不同的观测者对于这件事情的发生有没有争议？没有争议，因为这发生在很小的一个空间范围内，又是在很短的时间间隔内，所以这可以看成一个事件。一个事件发生与否，不同的观测者是没有争议的。 

那么就只能是：在两个不同的地点，同时的概念有可能会出问题。我们直观的想象中，即使地点不同，同时的概念也应该合理，对不对？但是爱因斯坦不这样想，爱因斯坦要从物理上去定义不同地点同时的概念。和之前一样，我们先随手“抓”过来一个定义，然后把它推广到一切可能的定义。 

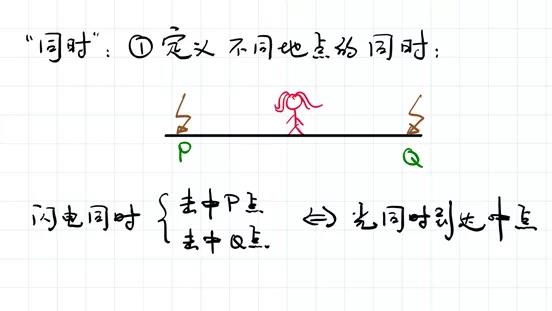
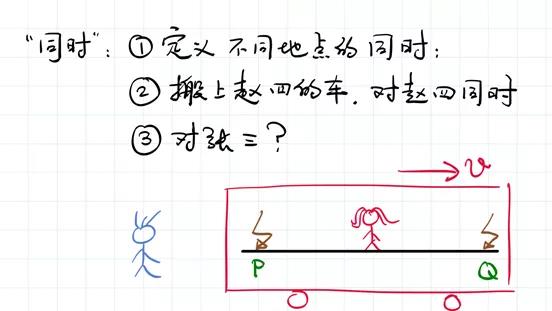
首先我们随手抓过一个什么样的定义呢？假如空间中有两个点P和Q，怎么定义在P和Q这两点上发生的事件是同时的呢？比如说有两个大雷，一个打在了P点，一个打在了Q点，雷打到P点会发出闪光，闪光会传到线段的中点，雷打到Q点也会发出闪光，闪光也会传到线段的中点。如果站在线段中点的赵四同时看到了 P和Q发出的闪光，那就说雷打到P点和打到Q点是同时的。这是同时的一个定义。 

下面我们根据同时的这个定义，看一看有两个观测者，他们的运动状态不同的场景。和上一节考虑时间间隔一样，我们还是用4步推理的方法。

首先，我们已经定义了同时性，我把它画到一个图里，这个图我们叫“时空图”。横坐标代表的是空间，纵坐标代表的是时间，但是时间上面我们乘了一个光速c，这样的话，横纵坐标的单位就一样了，并且在 x和ct的图上，光线运行的轨迹是沿着45度角线。

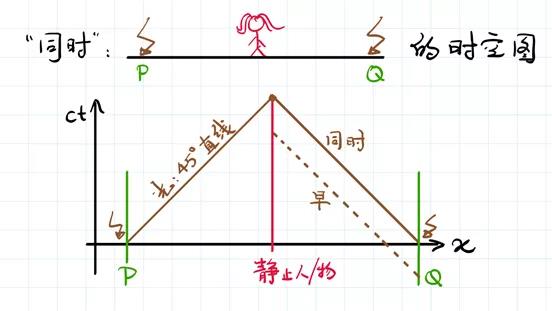
那么刚才我讲的同时的概念，在时空图上画出来是什么样子的呢？在时空图上，首先雷打到了P点，也打到了Q点，然后 P点和Q点的光线，就向着中间的赵四传播。光线传播是沿着45度角方向。如果这两束光线同时到达赵四，那就是说，前面雷打到P点和打到Q点的时间也是相同的。如果不相同的话会出现什么样的现象？比如说，如果这个雷是先打到Q点的，会出现什么现象呢？那么光线从Q点传播到中间的赵四，就会早一些，对不对？

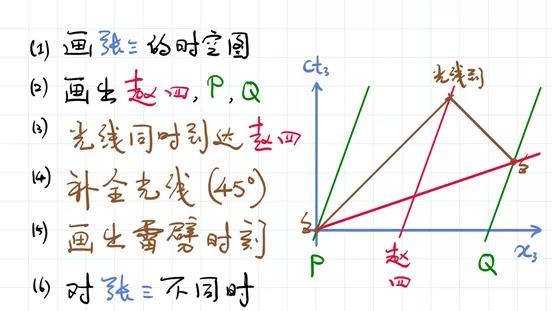
说了半天，你可能感觉我说的全是幼儿园都知道的废话，但我们再往下走一步，就不是废话了。我们把前边同时的定义运用到作匀速直线运动的赵四的车上。根据运动的相对性，按照前边同时的定义，如果在地上看，雷打到P和Q是同时的，那么在赵四的车上也是这样的。现在问题来了，相对于张三，这两个雷是同时打到P点和Q点的吗？为了回答这个问题，我们去画张三的时空图。横坐标是张三的空间，纵坐标是光速乘以张三的时间。 

在这张图上画出来是什么样子的？首先我们先画出赵四以及P、Q点的运动轨迹。赵四和P点、Q点都在赵四的车上，作匀速直线运动，相对于张三来讲，赵四运动的轨迹是一条斜线，如下图所示。P点和Q点也是一样的。

对于赵四而言，光线同时到达赵四意味着什么？我们把光线往回画，看光是什么时候发出来的。沿着45度角的线向回追溯和 P、Q的运动轨迹的焦点，即雷打到P点和打到Q点的时刻。这个雷劈的时刻，对张三而言，在张三的ct3轴上，是不是早一点？也就是说，两个点虽然相对于赵四是同时的，但是相对于张三不是同时的。P点事情发生的早，雷打到P点更早，而雷打到Q点更晚。也就是说，用我们前面的同时的定义，这个同时是相对的。

第4步和前面钟慢的分析是一样的。前面我们用了一种特殊的同时的定义，但对于所有可能的同时的定义，只要这些同时的定义在地面上的实验是自洽的，那么搬到赵四的车上之后，所有的同时的定义都会给出：相对于赵四是同时的，但是相对于张三不是同时的。为什么？如果有一个实验告诉我们，相对于张三和相对于赵四都是同时的话，那么在赵四的车上看，这个实验和我们定义出来的两个雷打到P点和Q点的实验得到的结果是不是就不一样了？这就违背了相对性原理。

所以说，前面看似随意的一个同时的定义是普遍的。也就是说，同时的概念对于不同的点而言是相对的。

我们再考虑一个相关而稍稍有点区别的问题：在张三的坐标系中，我们如何画出赵四的坐标系？什么叫赵四的坐标系？首先，赵四的时间轴在哪里？赵四的时间轴就是赵四的空间坐标为常数所对应的线。赵四相对于他自己是不运动的，所以说赵四的时间轴就是赵四的空间坐标为常数时的线，即ct4这条线。赵四的空间轴在哪里呢？同样，赵四的空间轴是赵四的时间坐标为常数所对应的线。前面那两个大雷打到P点和Q点对赵四而言是同时的，把那两个点连起来就好了。现在的时间轴和空间轴是不是很不一样，空间轴是翘起来的，时间轴是趴下去的。

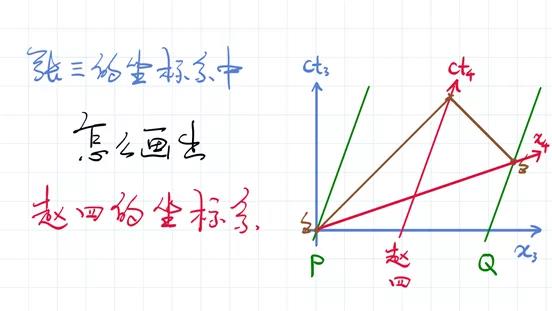
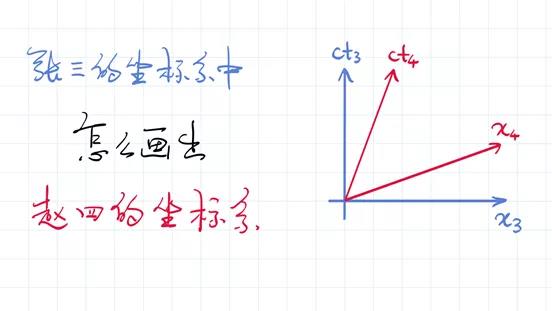
原则上，我们可以问这样一个问题：如果有一个点，这个点我们知道它在赵四的参照系下的坐标t4和x4，那么这个点在张三的参照系下，坐标t3和x3是多少呢？这个问题其实要经过一些计算，我们才能回答的，在这里我们就先不回答了，但是它的答案就是著名的“洛伦兹变换”，非常有用的一个数学关系。 

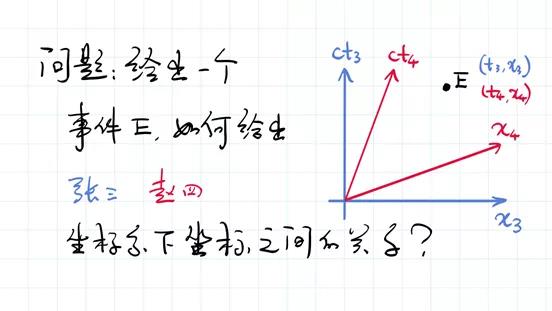
我们回到之前讨论过的一个问题，叫做“双生子佯谬”。前面我们讨论过，如果张三和赵四本来一样大，同时出生，现在张三和赵四有相对运动。有相对运动之后，张三看赵四的时间变慢了。运动是相对的，所以说赵四看张三的时间也变慢了。到底是谁变慢了呢？我们可以说，他们看对方的时间都变慢。都变慢了会不会有矛盾，在他们遇上的时候，他们比较时间，是不是就露馅了？ 

但是如果两个观测者一直是匀速直线运动的话，他们最多碰见一次，出生的时候他们确定他们的年龄是一样的，碰见一次，然后他们就再也碰不上了。所以说，这个戏永远也不可能穿帮。

但你可能就要问了，如果赵四是远离张三运动，但是运动到一定的时间，它忽然停住，然后再返回来，这样会出现什么样的现象？这样不就碰见两次了吗？当第二次碰见的时候，到底是张三的年龄更大，还是赵四的年龄更大呢？

这里可以给出两个答案，一个是鸵鸟型答案，一个是更认真一点的。

鸵鸟型答案说，首先张三看赵四在运动，所以说赵四的时间变慢了，所以回来的时候相对而言赵四是更年轻的。因为张三一直是一个惯性观测者，张三的运动状态没有改变，所以说我们可以相信张三的结论。而赵四呢，在运动出去和运动回来的节点上，他必须要经历一个减速、加速的过程。所以，赵四并不是一直在一个惯性系里面，前面我们推导的钟慢的效应对赵四并不是一直成立的。所以，最后两个人遇上之后，是张三变得更老了，赵四的时间流逝更慢。

这个答案可能大家听得有点云里雾里，我是禁止大家从这种角度去解答的。但是大家可以思考一下，赵四会看到什么样的现象呢？虽然赵四经历了一个加速，但是我们可以通过张三去推测，在赵四的参考系下发生了什么样的现象？

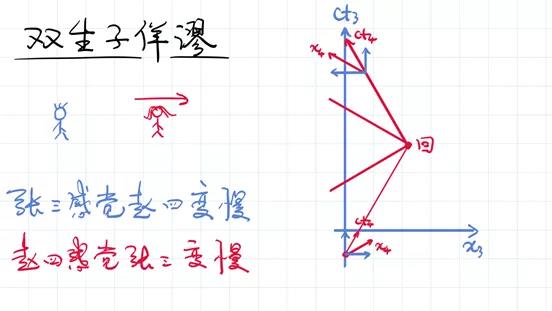
首先，在赵四远离张三的过程中，赵四的时间轴和空间轴分别是什么？【以下参见视频】这个是时间轴，这个是空间轴。记着这个空间轴就是同时的线，也就是说当赵四要返回但是还没等返回的时候，赵四的空间轴是这样。那么在赵四返回的过程中，赵四的空间轴，也就是赵四时间相等的是哪一条线呢？是这样的线，也就是说赵四刚刚开始返回的时候，对于赵四而言，时间相等的线是这样的线。换句话说，在赵四返回的那一刹那之间，他的参照系有了一个巨大的变化。这个巨大的变化使得时间有了一个巨大的差别。 

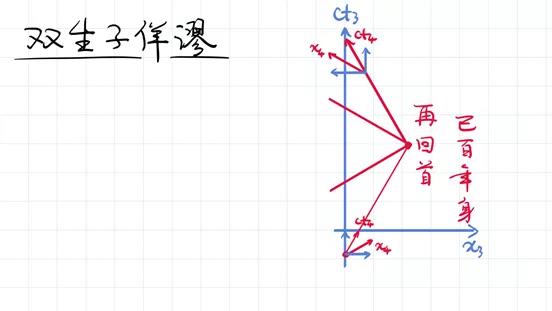
回头这一点非常重要，“再回首已百年身”，“红颜弹指老，刹那芳华”。这一点给人的感觉还是挺悲凉的。因为相对论告诉你时间旅行是可能的，你想到多远就可以跑到多远。但是当你一回头的时候，你所认识的一切的人已经都不在了，已经都不在你的参照系里，他们都已经过了成百上千，甚至上万上亿年，已经灰飞烟灭了。所以说，宇宙的时间旅行、空间旅行在相对论里虽然可能，但是结果可能并不是我们最初想要的。 

（责任编辑：杨玉露）

（版权说明，转载自：墨子沙龙公众号）