（本视频链接为https://v.qq.com/x/page/a31557173fx.html）

在狭义相对论中，信息的传播速度不能超过光速。大家可能会提出一个问题：假如张三和赵四相距一光年，两人之间有一个杆，张三抓着杆的一端，赵四抓着杆的另一端，那么是不是两人可以通过推拉这个杆去传递信息？ 

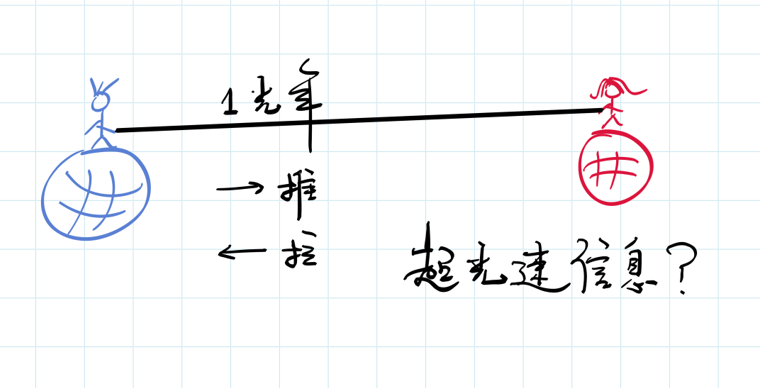
网上搜一下，会发现这个问题被问了无穷遍，而张三和赵四之间那也是刀、枪、剑、戟、斧、钺、钩、叉、镗、棍、槊、棒、鞭、锏、锤、抓、拐子、流星，十八般兵器，样样都被问到了。那么，这个问题是不是反对了相对论？

其实并不是，为什么？张三推这个杆会发生什么现象？杆离张三近的这一端，密度会变大。而密度变大的改变在杆上的传播速度是不会达到光速，更不会超过光速的。对于一光年的杆，需要一年以上的时间，杆上的推拉变化才能传到赵四。

不讲十八般兵刃的话，我们还有一样兵器——拳头。张三挥一挥拳头，赵四那边会有什么影响？假如牛顿的万有引力定律是对的，那么张三挥一挥拳头，在赵四那边，引力的方向甚至大小立刻就会产生一点变化。为什么？张三的拳头有一个质量，不管这个质量有多大，总之是有一个质量的。这个质量在赵四这边就会产生一个引力。根据牛顿的万有引力公式，拳头的位置不同，马上就会在赵四那边反映出引力的不同来。

当然这个变化是非常之小的，但是对于赵四可以测得无穷精确的理想情况，通过张三挥动拳头，赵四瞬间就可以得到张三的信息了。这是不是反对相对论了？ 

如果你认为牛顿的万有引力公式是成立的，那么这还真的就反对狭义相对论。也就是说，狭义相对论和牛顿的万有引力公式是矛盾的。怎么办？ 

爱因斯坦为这个问题困扰了很久。我小时候读过一个版本的《爱因斯坦传》。这个《爱因斯坦传》里有很多比较狗血的故事，其中一个故事是：

爱因斯坦和居里夫人去登阿尔卑斯山。他们到了山顶，这时爱因斯坦俯视从山顶向下的缆车，忽然心里想象到了一个图景：如果缆车的线断了，缆车车厢忽然从半山腰就掉下来了，这样的话，会发生什么样的事情？有感而发，爱因斯坦马上拉住了居里夫人的手，说：“我找到了，我终于找到了。”还没等居里夫人惊呼出来，爱因斯坦就说：“我终于找到了引力的秘密

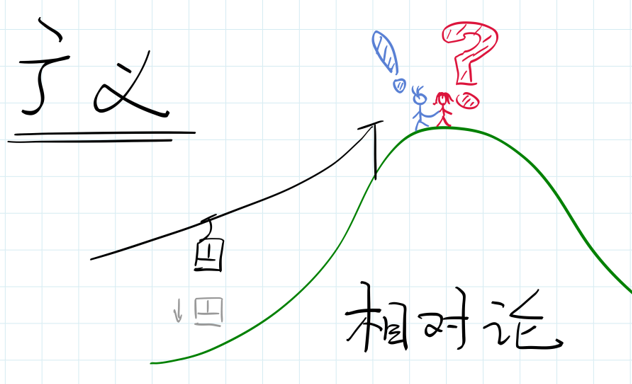
后来我又读了好多爱因斯坦的传记，并且查了好多传记里边相关的部分，其实并没有这么狗血的记载。但小时候我就偏偏看到了这样一本书，并且我后来选择去研究物理，可能很多也是受了这本书的影响。当然了，受这本书的影响并不是说想去抓哪一个女科学家的手，而是这本书里还有很多其他的狗血故事。

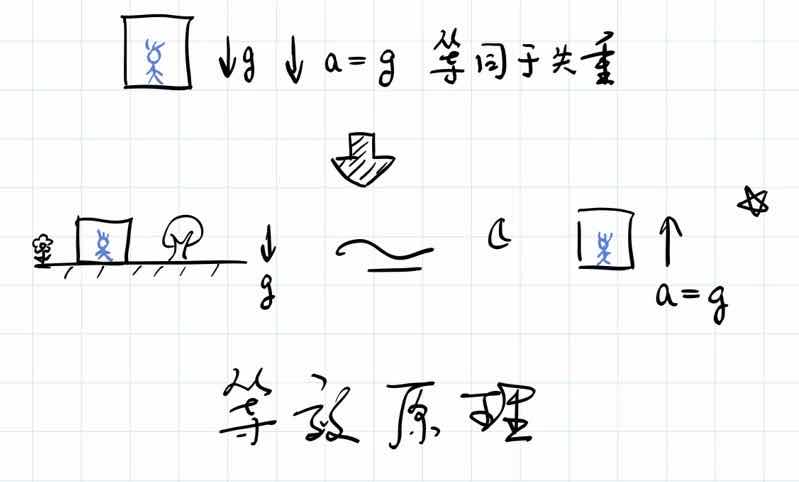
但是无论如何，坠落的缆车也好，坠落的电梯也好，爱因斯坦确实想到过这样一个图景。当想到这个图景，他无比激动，感觉找到了引力的奥秘。那么，他找到的是什么呢？他想到的是，如果一个人在缆车里自由下落的时候，他能不能感受到引力？感受不到引力，也就是说，他处于失重的状态。当然，大家理论上想一想就行了，不要真的去自由下落，因为最后你落到地上的时候，终究是要感觉到冲量定理的。

自由下落的时候，加速度的效应和引力的效应可以抵消，爱因斯坦从这一点出发，并进一步去想：1）一个电梯放在地上不动，2）电梯在宇宙空间之中，周围没有地球、没有引力，但是电梯在向相反的方向加速，这两种情况也是完全等价的。因为情况1是相当于引力被同样方向的加速度给消掉了。 

换一种想法，引力可以用相反方向的加速度完全的模拟出来。这个思想最早并不是爱因斯坦想到的，伽利略就曾经这样想过。据说，伽利略做了一个比萨斜塔实验，把一个大铁球和一个小铁球从比萨斜塔上扔下来（据说这一段其实也是编的，但是无论如何，伽利略想过这个问题）。不仅如此，伽利略还想过，如果材料不同的话会怎么样：如果是一个大铁球和一个大铜球一起扔下来，也应该同时落地。这就是等效原理的雏形。 

我们知道，牛顿把伽利略的理论进行了数学化，牛顿第二定律说：力和加速度之间的比值是质量。这个质量叫做惯性质量。我们还有万有引力定律，当中力是和物体的质量成正比的，我的质量大一点，我就受到的地球引力多一点，这儿也出现了一个质量，这个质量叫做引力质量。我们想一想，在表面上看，惯性质量和引力质量是不是看起来没什么关系？一个是说我改变运动状态的难易程度，这个是惯性质量，另一个是说我受到引力的大小和我的一个性质有关，这叫引力质量。他们俩之间看起来有关系吗？没有关系。

但是牛顿发现这两个量是相等的，或者至少来讲这两个量是成正比的，这个比例系数我们可以给它调成是相等的。这件事情，牛顿自己就已经感觉到是非常的不可思议了。牛顿用各种各样的材料去做实验，比如金、木、水、土，就差没用火；还用了银、盐、玻璃、羽毛等各种各样的东西做了实验，发现惯性质量等于引力质量的规律对这些东西都是成立的。

有人问，牛顿上哪儿找的这些奇奇怪怪的东西去做实验呢？有人说是因为牛顿在研究炼金术，他想把后边所有的东西都练成金子。后来他失败了，没有把这些东西炼成金子，但是至少证明了这些东西在一定程度上和金子是等效的——在惯性质量等于引力质量的程度上，和金子是等效的。

虽然说爱因斯坦并没有发明这个原理，但是他看到了等效原理背后所蕴含的深刻的物理意义。首先，等效原理告诉我们，引力的效果可以由一个反向的加速度的效果完全的模拟出来。有一个所谓的奥卡姆剃刀原理，就是“如非必要，勿增实体”，如果说引力和加速是一回事的话，我们干嘛还要两个概念？或者说引力，现在严格来讲是均匀的引力，它和加速，我们只需一个就好了。哪一个？加速这个概念体现了运动时空的本性、看起来比较基本，我们就要加速这个概念。 

这样的话，均匀的引力这个概念我们可以抛弃掉，或者说这个概念只是我们的一个幻觉而已。这就解决了前面说的牛顿引力超距作用这个问题。怎么解决的？你不是用引力反对我的相对论吗？现在连引力这个事儿都没有了，你还用什么来反对相对论？所以说，等效原理是爱因斯坦去解决牛顿引力和狭义相对论的矛盾的一个突破口。 

当然了，这是一个过于简化的讲述，从这个突破口开始，还有很多很多的其他的事情，尤其是空间弯曲的事情。这个我们后边再讲。不过有了一个突破口，爱因斯坦找到了可以努力的方向。等效原理，虽然它只是广义相对论走的一步，是一个突破口而已，但是有了等效原理，立刻我们就可以理解一些现象。比如，光线在均匀的引力场之中会偏折吗？ 

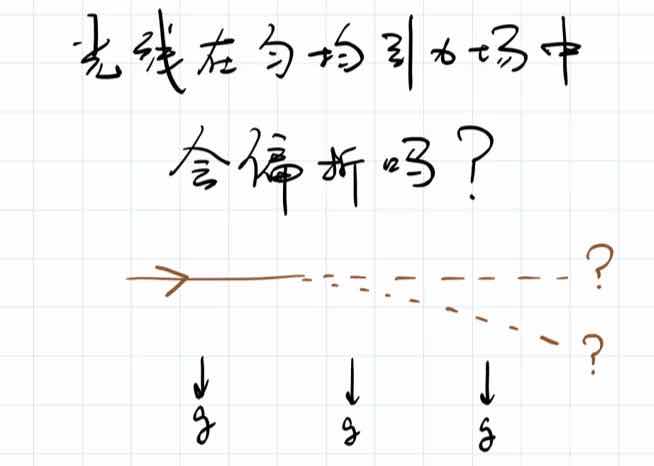
在牛顿引力的框架中，这个问题会比较困惑。因为牛顿引力里，根本就没有说牛顿引力对光是什么样的作用，而我们知道了狭义相对论以后，一定程度上就知道了，光是没有质量的，牛顿说引力是作用于质量的，那么既然光是没有质量的，是不是牛顿引力里，光线不应该在引力场中偏折？或者更严格的说，在牛顿引力里，光能不能在引力场里偏折，其实是一个没有很好定义的一个概念。 

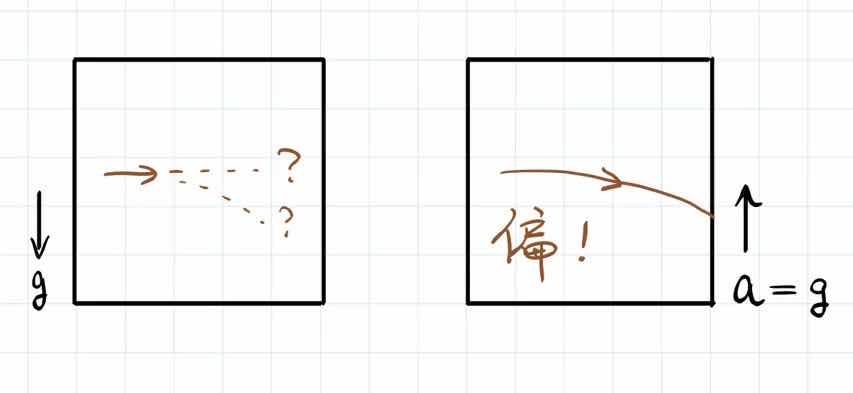
但是，我们有了广义相对论的这第一步，等效原理，我们就可以知道光是不是应该在引力场中偏折。我们虽然不知道在有引力的时候，光应不应该偏折，但是——第一，我们知道有引力的情况等价于有反向加速的情况；第二，我们知道如果有反向加速的话，那么电梯就在向上运动。电梯开始的时候没有运动的话，因为有加速度，电梯也渐渐的开始向上运动。当电梯向上运动的时候，光相对于电梯是不是偏折了？如果你不往外边看的话，那么是不是相当于你就发现了光是偏折的？也就是说我们等效回来，通过等效原理就知道光在引力场当中应该是偏折的。

这就是广义相对论的第一个预言。有了预言以后，大家就需要去实验观测光在引力场中的偏折。在我的周围找一个光，看看它偏折不偏折，这行不行？不行，因为我的质量太小了，光偏折的效应可以忽略不计。

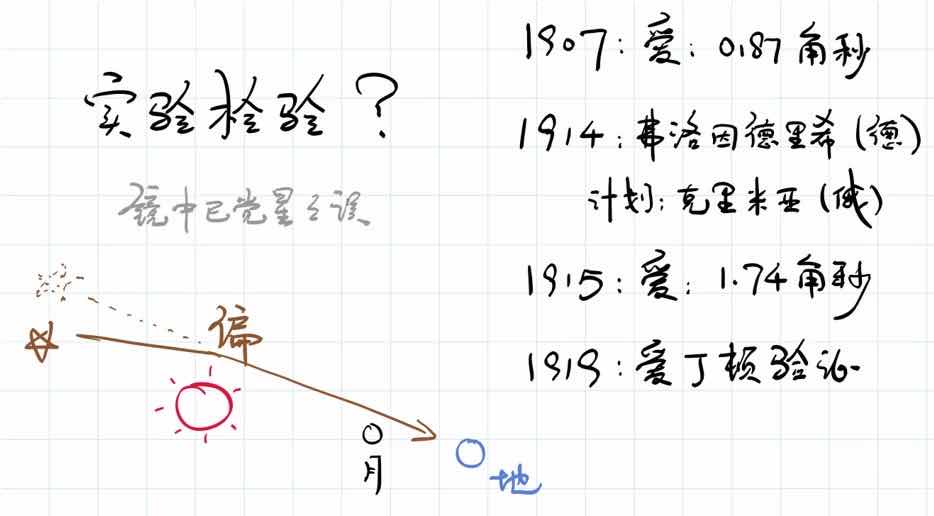
在我们生活的周围，质量最大的是什么东西呢？也就是说，光线偏折效应最明显的是什么东西？就是我们的太阳。那么我们就研究一个星星经过太阳的时候，它的星光从星星到太阳再到我们，是不是会偏折呢？这就有了一个问题，你研究星光经过太阳的时候是不是偏折，但是你白天有看见过星星吗？尤其是你白天能在太阳附近找到星星吗？这是不可能的事情，太阳太亮了，对不对？怎么办？我们把太阳挡上就行了。怎么把太阳挡上？就是日食。在日全食的时候，我们就有希望去观测太阳附近的星星，其光线传到我们的过程中，如何被太阳所偏折。

爱因斯坦在1907年基于等效原理，通过均匀引力场的预测，计算出偏折是0.87角秒。1914年，有一个物理学家叫弗洛因德里希，他打算去做这个实验。他是一个德国人，我们知道日全食并不是整个地球马上全都日全食的，是在地球中某一些区域才能看到日全食，怎么办呢？这个德国人就跑到俄罗斯的一个小岛克里米亚去测量日全食。结果日全食还没开始，第一次世界大战先开始了，弗洛因德里希也被俄国抓了起来。所以他就没有测量到日全食，也没有测量到光线偏折的效应。

到了1915年的时候，爱因斯坦发现自己算错了。这并不是说他出了一个简单的计算错误，而是他发现，其实用均匀的引力场来近似太阳的引力场是不全面的，我们还应该考虑空间弯曲的效应。

讨论空间弯曲的效应之后，这个偏折角度变成了原来的二倍，从0.87角秒变成了1.74角秒。1.74角秒的数值，在1919年被爱丁顿爵士在日全食观测中所验证。这件事情真的很神奇。爱因斯坦也很幸运，如果1914年弗洛因德里希发现了光线的偏折不符合爱因斯坦的预言，然后爱因斯坦再去修改他的理论的话，其时广义相对论看到光线偏折就不再是一个预言了，这是一个所谓的postdiction，就是说马后炮。

知道了光线偏折，我们有什么应用？这个应用就是，你们一帮人合影的时候，你可以适当的往后站一站。因为光线经过前边人会偏折一点，这个偏折会造成你看起来会比你应该有的高一点。当然了，高的实在是微乎其微的那么一点点。如果你不在乎的话，我可以悄悄的告诉你，其实站后边也可以显脸小。

除了光线偏折之外，在均匀的引力场中，我们还有一个效应，就是：时间的流失速度，在引力势低的地方和引力势高的地方也是不一样的。具体一点，比如说赵四站在高一点的地方，而张三站在低一点的地方，然后赵四向张三发射了一束光，这束光从开始发射到结束，它经历的时间是Δt₄。下面问题是：Δt₄这一段的光线，当它到达张三的时候，张三看到这一束光经历的时间Δt₃应该是多少？在引力场里边怎么回答这个问题？其实我们不知道怎么回答，对吧？引力场太神秘了，我们不知道它的物理规律，但是等效原理可以把这个问题等效成没有引力场但我们处于一个向上跑的电梯当中的情形。

向上加速的电梯当中，在加速的电梯里边，当速度等于0的时候，赵四向下发射出这样的一束光线。那么到达张三的时候，Δt₄变成了张三那边的Δt₃是多少呢？我们发现在赵四发射光的时候，电梯还没有跑，对不对？但是有加速度了。当张三接收到这束光的时候，电梯已经有了一个向上的速度。这个向上的速度说明什么呢？就是说当张三接收到这束光的时候，是张三和光在相向而行。相向而行的话，是不是Δt₃就比Δt₄小了？也就是说，赵四的一段时间在张三看来变短了，这就是引力场中的时间膨胀收缩效应。

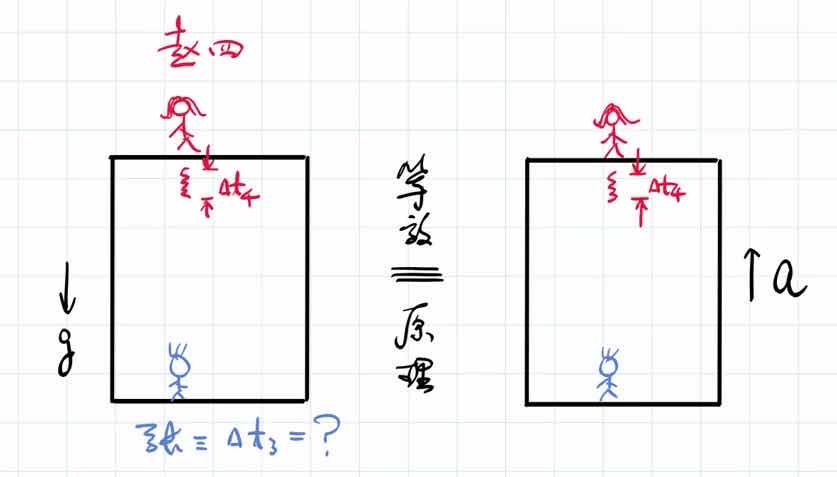
一个方便记住这个效应的方法是，当你处的位置比较高的时候，你就老得快。比如说，我楼上两层就是我们院长，然后再楼上一层就是校长，所以说，学校的高管翻译成英文叫senior management。这个翻译现在开来还是有一定的道理的。 

好，做一个小结。首先，狭义相对论和牛顿的引力是有矛盾的，因为牛顿的引力告诉我们引力是瞬时的，但是狭义相对论又告诉我们，没有瞬时的信息传递，信息的传递速度小于光速。这个问题怎么解决呢？等效原理。等效原理告诉我们，至少对于均匀的引力场，我们可以通过加速把引力的效应消掉。既然引力连效应都没有了，它就没有办法拿出来反相对论。当然如果你问不均匀的引力场的话，之后课程我们会讲。然后，我们讲了由等效原理推导出来的两个效应：一个是“后排显个高”效应，也就是光线偏折，另一个是“楼高老的快”效应，也就是时间膨胀。 

（责任编辑：杨玉露）

（版权说明，转载自：墨子沙龙公众号）