本次内容来自系列视频课程

“一说万物：现代物理学百年漫谈”

第八讲：广义相对论

8.2弯曲时空，引力退散

（视频链接：https://v.qq.com/x/page/a3158y35m56.html）

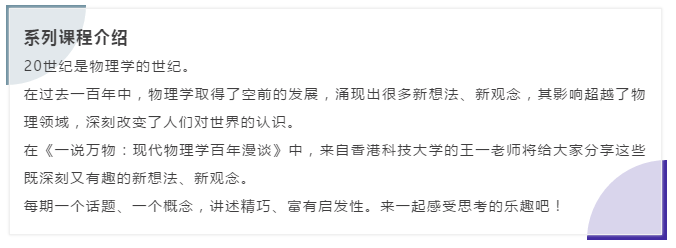
上一讲我们介绍了广义相对论中的等效原理，即我们考虑一个加速观测者的参照系，在这个参照系中可以把引力消掉。从这个角度上讲，引力看起来是一种幻觉。

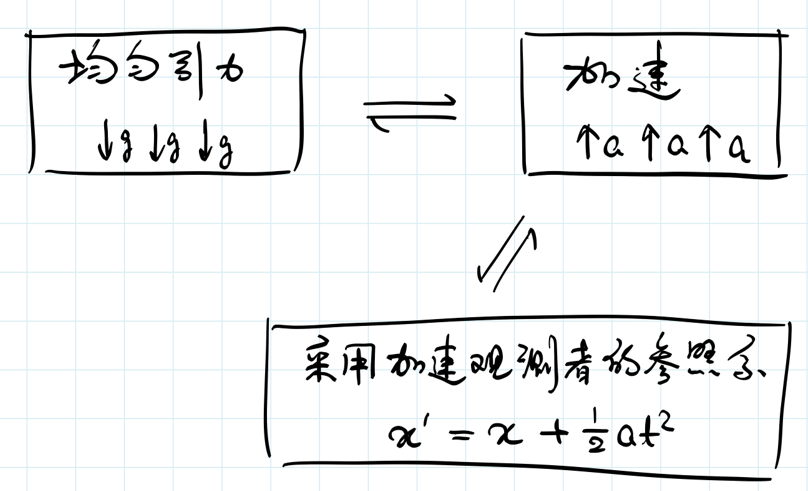
这里就有两个问题。第一个问题，我们考虑的其实是非相对论的速度，我们还可以考虑快一点的速度，这样，我们写公式的时候，可以写相对论性的加速度公式。当然，这是一个技术问题。

还有一个更重要的问题：前面我们一直假设引力场是均匀的，如果引力场不均匀，会出现什么现象？所谓“不患寡而患不均”，不均匀的引力场是有关“引力到底是不是幻觉，引力到底能不能消掉”的一个更本质的问题。

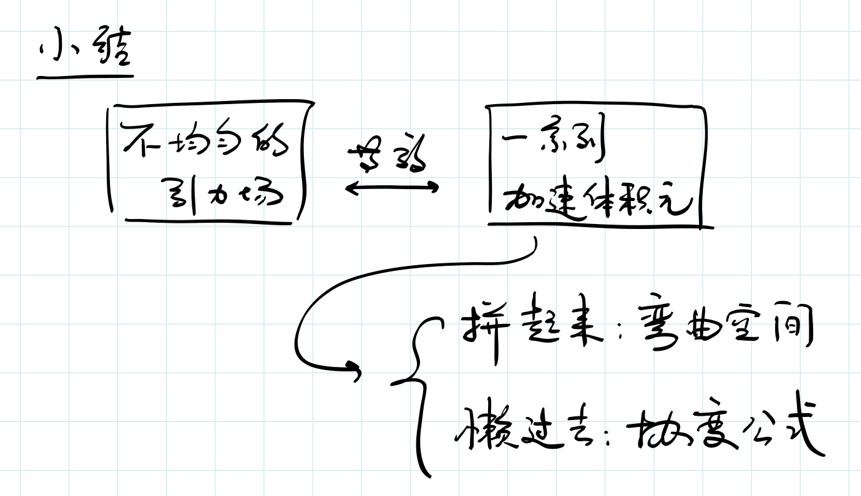
那么，不均匀的引力场我们怎么处理呢？我们用分而治之（divide and conquer）的策略：一个大的问题解决不了，我们就把它化成小的问题来一个个解决。这一思想在各个学科中都有体现，比如数学中的微积分思想，把整体函数的变化体现成一个个小量的分析。对于不均匀引力场，我们也可以用分而治之的策略：首先把问题分解成足够小的问题，解决了每一个小问题之后，再看一看怎么把这些小问题的解决方案拼成一个完整的解决方案。

引力退散指南

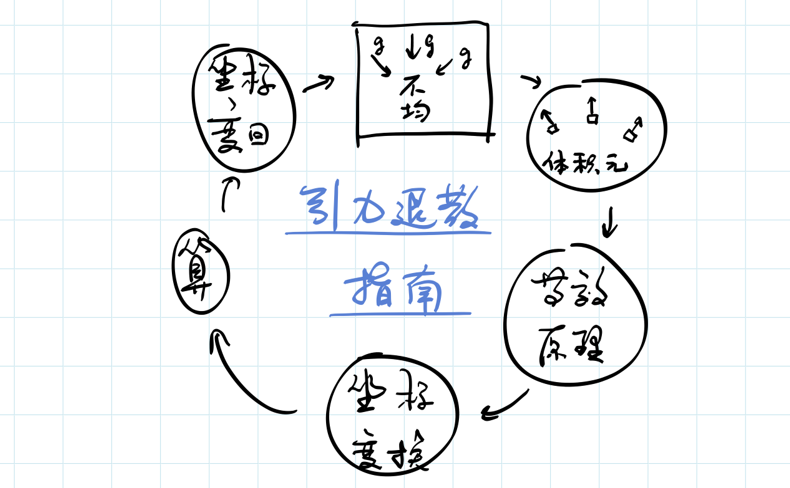
我们去观察一下：不均匀的引力场具有什么性质呢？除了量子引力暂且不讨论之外，其他的不均匀引力场都有一个共同的性质：当我们看越小的空间尺度时，这个不均匀引力场的不均匀性也越小；当我们看足够小的空间尺度时，不均匀性就可以忽略了，我们看到的其实是近似均匀的引力场。

举一个例子，空间站上的宇航员以一个相当大的跨度去看地球的引力场，他看到地球的引力场是向着地心的，是不均匀的引力场。但对于一条躺平的咸鱼，它感受到的地球引力是相当均匀向下的，而不是那种非常不均匀、朝着地心让我撅起来的引力场。

所以说，考虑的尺度越小，引力场越均匀。这样，我们就可以把一个不均匀的引力场近似成在每一个微小的体积元之上均匀的引力场。然后我们把等效原理应用到这些微小的体积元之上：在微小的体积元上，向下的引力用向上的加速来替代，于是在微小的体积元上，我们就把引力消掉了。即，在每一个微小的体积元上，我们做一个独立的坐标变换。这个独立的坐标变换相当于在每一个微小的体积元上有一个独立的加速观测者用来消除引力。这样，引力在空间当中的每一点都消掉了。

如果我们考虑在引力场中物体的运动，比如引力场中一个小球的运动、光线的运行、电磁现象等等，我们都可以将空间逐块考虑。这样，原则上对于全空间当中的每一点，我们都可以知道小球是如何运动的、电磁场是如何变化的，等等。全空间中每一点都知道了，那么全空间其实我们也知道了。最后，我们再把空间中的每一点通过坐标变换，变回到以前的坐标，这样我们就知道了在一个所谓的引力场当中，小球、光线、电磁场是怎么运动的。关键就是分解成体积元，分别应用等效原理，最后再变回原来的不均匀引力场。

这个办法是非常巧妙的，也是广义相对论的精髓，但是这个办法给我们带来了两个值得思考的问题。

第一个问题。我们把引力场分解成了一个个小的体积元，这些体积元之间是什么关系？如果我们想有一个整体的物理图像，我们需要把这些小的体积元一个一个的粘起来，这些小的体积元粘起来以后，形成什么样的空间呢？你可能想当然地认为，应该还是原来的空间。其实不一定，比如足球是由一块一块很小的、比较平的皮子缝起来的，但是缝起来之后，就形成了一个表面弯曲的、球形的足球。我们的空间也是这样，我们考虑空间中每一点很小的具有不同运动状态的体积元，把它们粘回来，我们发现最后的空间其实是弯曲空间。不均匀的引力场导致了空间的弯曲。

其实弯曲的不只有空间，弯曲的是整个时空。在时空的时间方向上，不均匀的引力场也导致了弯曲，即我们前面讲到的引力场中的时间膨胀现象。比如在太阳的引力场中，在太阳附近有三个事件，从离太阳越远的观测者去看，这三个事件的时间间隔看起来就越长。这就是引力场中的时间膨胀效应，可以看成是：在引力场中，时间也弯曲了。

引力场中的时空弯曲其实就是有质量物体感觉到引力的根源。牛顿引力就是引力场中的时空弯曲做一个非相对论近似的结果。

第二个问题。你可能会觉得这一套手续简直太麻烦了：先要做一个坐标变换，空间中每一点去选择不同的参照系，最后计算完以后，还要把空间中的每一点这无穷多的参照系都给变回到原来的参照系当中。这简直太麻烦了！我懒，不愿意做这样的事情，那怎么办？其实懒也是个好事情，一定程度上讲，懒是人类很多科学技术进步的动力。

做坐标变换的时候，其实我们就可以想一个问题：是不是有一些东西可以在坐标变换的时候不变呢？比如在极坐标（polar coordinate）下，我画了一个北极熊（polar beer）。那么，polar coordinate下边的polar beer在笛卡尔坐标系（Cartesian coordinate）下应该是什么样子？应该是一个Cartesian beer，还是仍然是一个polar beer？其实还是那个北极熊，还是那个polar beer。也就是说，在坐标变换下，图像本身应该是不变的。

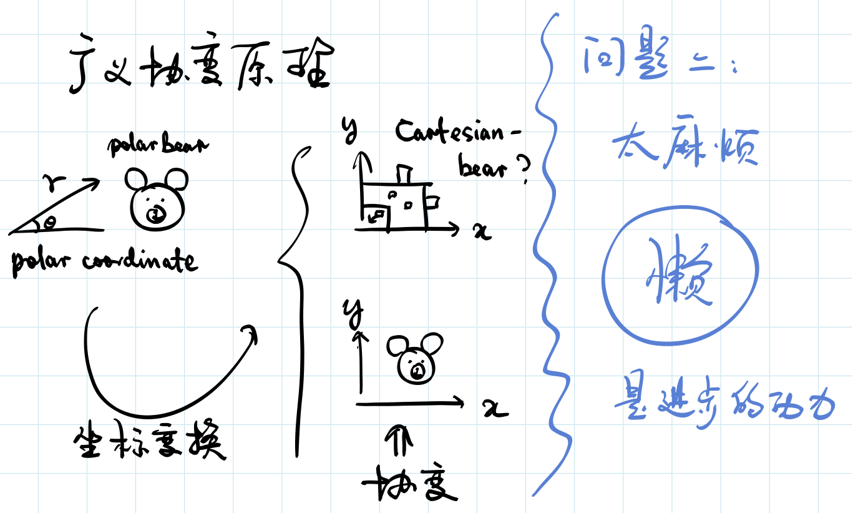
当然图像是一个非常具体的概念，但我们也可以进一步发问：是不是可以找到一种公式体系，让方程也在坐标变换下是不变的？如果我们能找到这种坐标变换下不变的形式，那么我们就不用把坐标来回变，而直接用这种坐标变换下不变的方程组形式就直接能从平坦空间推广到不均匀引力，即推广到弯曲空间。

这种坐标变换下不变的方程组是可以找到的，这就是广义协变原理。其中的数学结构是非常优美的，但是在这里我们就不具体描述了。

导师简介

王一：中国科学技术大学本科，中国科学院理论物理研究所博士。现任香港科技大学副教授，研究领域为理论宇宙学。近期的主要研究兴趣是将物理学中最大的物体和最小的物体联系起来，用早期宇宙的遗迹研究基本粒子物理。其他研究方向还包括早期宇宙模型、暗能量、暗物质、原初黑洞、引力波等。曾获香港大学教育资助委员会青年学者奖、被学生评选为最喜欢的教师。

责任编辑：杨玉露）

（版权说明，转载自：墨子沙龙公众号）