看，温度远去了，你能听到吗 | 中国科大量子模拟团队成功测量第二声衰减

中国科学技术大学潘建伟、姚星灿、陈宇翱等与澳大利亚科学家胡辉合作，首次在处于强相互作用（幺正）极限下的费米超流体中测量了第二声波的衰减率，揭示了在该系统中存在着一个可观的相变临界区，并获得了趋于量子力学极限的黏滞系数与热导率。该项工作为理解强相互作用费米系统的量子输运现象提供了重要的实验信息，是利用量子模拟解决重要物理问题的一个范例。2月4日，该成果以长文（research article）的形式发表在国际权威学术期刊Science上[Science 375, 528-533(2022)]。

与宏观现象不同，描述微观世界物理规律的是量子力学。由大量的、遵从量子力学的微观粒子组成的系统称为量子多体系统，与量子多体系统的性质和行为有关的问题称为量子多体问题。这是一大类很重要的物理问题，包括高温超导的机制、宇宙在诞生初期的演化等等。在量子多体问题中，当微观粒子之间的相互作用比较微弱时，解析方法尚有一战之力；一旦相互作用较强，不仅解析求解举步维艰，而且基于经典计算机的数值模拟方法亦是捉襟见肘——因为随着粒子数的增加，计算所需要的资源将呈几何式增长。那么，我们不妨“使用魔法打败魔法”，借大自然之矛攻大自然之盾；这就是量子模拟的初衷。

量子模拟，顾名思义，“量子”表示涉及的基本规律是量子力学，“模拟”意指构造并研究一个与原问题本质相似但是更容易解决的问题。一个与“模拟”有关的著名例子便是风洞——在设计飞行器的外形时，风洞实验就是对真实的空气动力学问题的模拟。之所以量子模拟被寄予厚望，是因为量子力学在原理上就赋予了模拟方法以得天独厚的条件。在量子力学中，有一个至关重要的物理量叫做哈密顿量——一个量子系统的性质和演化都由其哈密顿量所主导。故而，如果两个量子多体系统的哈密顿量别无二致，那么我们一旦把其中一个系统研究清楚，就可以知晓另一个系统的性质和行为。此诚可谓“败也量子，成也量子”是也。

我们今天要详细介绍的，是用量子模拟的方法来研究一个量子多体系统——强相互作用费米超流。

1911年，荷兰科学家卡莫林·昂内斯（Heike Kamerlingh Onnes, 1853-1926）发现了超导现象，揭开了低温物理学的新篇章。低温物理学的另一个里程碑是1937年苏联物理学家卡皮查（Пётр Леонидович Капица, 1894-1984）在液态氦-4中首次发现了超流现象。液氦超流具有一系列奇特的性质，比如：可以通过极为细小的毛细管而不呈现任何粘滞性；拥有极高的热导率，约为室温下铜的800倍；可以克服重力而不断沿着容器壁向上攀升；能够产生量子化的涡旋晶格；存在后文将要重点介绍的第二声波，等等。苏联著名的物理学家朗道（Лев Дави́дович Ланда́у, 1908-1968）建立了二流体模型，从宏观上很好地解释了液氦超流的诸多性质。二流体模型认为，液氦超流体中含有两种成分，一种是常规流体成分，具有黏性和熵，另一种是超流成分，无黏性且熵为零。正是超流成分的存在使得超流体如此与众不同。超流与超导都是宏观量子效应，二者之间有着千丝万缕的联系——比如，从某种角度来说，常规超导体中的超导现象可以看作是大量电子形成超流的缘故。直到今天，超流与超导依然是物理学研究的热点与前沿。

沿着器壁向上爬升然后溢出的液氦超流

自然界中的微观粒子可以分为费米子和玻色子两类，质子、电子都属于费米子，氦-4、钠原子都属于玻色子。两种不完全相同的费米子组成的多体系统有着丰富多彩的物理现象，比如，超导就与两种不同自旋的电子组成的系统息息相关。1957年，巴丁（John Bardeen, 1908-1991）、库珀（Leon Cooper, 1930-）、施里弗（John Robert Schrieffer, 1931-2019）三人正式提出了被后世称为BCS理论的超导原理，近乎完美地解释了有关常规超导体的实验结果。BCS理论指出，超导现象的关键之一在于电子发生配对；至于不能被BCS理论定量描述的非传统超导体，如铜基超导体等，电子配对的存在依然是科学界的共识。事实上，电子的配对是费米子配对的一个特例。另一方面，玻色子的有关理论的诞生则要早得多，并且远远超前于实验。1924年前后，爱因斯坦受到玻色的启发，发展了被后世称为玻色-爱因斯坦统计的理论，并且指出，全同玻色子组成的系统在温度足够低时会有宏观量级的粒子占据到系统的基态上，这种现象后来被称作玻色-爱因斯坦凝聚（Bose-Einstein Condensate, BEC）。直到1995年，美国科罗拉多大学Eric Cornell和Carl Wieman的研究小组才首次制备出了“真正的”玻色-爱因斯坦凝聚。

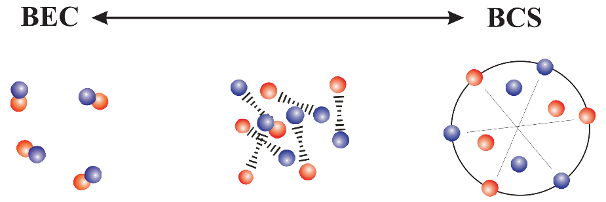
BCS-BEC渡越中两种费米子的配对

BCS超流和玻色-爱因斯坦凝聚二者看似毫无关联，实则可以纳入到一套统一的理论框架下——BCS-BEC渡越。对于一个由两种不完全相同的费米子组成的多体系统，在BCS极限下，两种费米子之间存在等效的微弱吸引力，进而发生长程配对并形成超流；在BEC极限下，两种费米子发生短程配对，组合成一个个玻色子，进而发生玻色-爱因斯坦凝聚。通过调节粒子间的相互作用，可以实现从BCS超流到玻色-爱因斯坦凝聚之间的平滑过度。虽然BCS-BEC渡越的有关理论早在五十多年前便已经提出，但是直到二十年前，超冷原子技术的发展才使得相关的实验研究成为可能。

在BCS-BEC渡越的中间，有一个非常特殊的存在——强相互作用费米系统。处于超流状态的强相互作用费米系统称为强相互作用费米超流。之所以冠以“强相互作用”之名，是因为组成多体系统的两种费米子之间的相互作用之强，已经达到了量子力学两体散射理论所容许的上限——幺正极限（unitary limit）。有鉴于此，强相互作用费米系统也被称为幺正费米系统。处于幺正极限下的相互作用导致粒子之间具有很强的关联性，这种强关联的一个重要的体现是，强相互作用费米超流的相对相变温度（超流/超导相变温度与费米温度的比值）很大，是常规超导体的数千倍，甚至比铜基超导体等高温超导体还要高出许多。对强相互作用费米超流的研究将对我们理解和探索高温超导体等强关联费米系统有所助益。强相互作用费米系统的另一个备受瞩目的特点在于，由标度不变性所导致的普适性——内能、熵等热力学状态函数以及黏滞系数、热导率等输运系数都只是粒子数和温度的函数，与粒子间相互作用的具体形式无关。

普适性是既有趣又有用的。在宇宙中，中子星是密度仅次于黑洞的星体，如果把地球压缩到和中子星同样的密度，那么这个“地球”的半径将只有22米。特别地，中子星的地壳就是一个强相互作用费米系统。此外，现代宇宙理论认为，在大爆炸后的数微秒内，宇宙中充斥着温度极高的夸克-胶子等离子体，这种物质形态也可视为强相互作用费米系统。还有我们接下来将要介绍的、通过超冷原子技术实现的强相互作用费米气体，其密度和温度都处在另一个极端——密度只有空气的百万分之一，而温度只比绝对零度高千万分之一摄氏度。纵然这三者看起来风马牛不相及，但是在强相互作用费米系统普适性的助力下，我们一旦洞悉了其中一个的性质，就对另外两个系统也有了深入的了解。换言之，三者之中任何一个系统都可以视为对另外两个系统的量子模拟。中子星是可望而不可即的，夸克-胶子等离子体的制备不仅非常困难、耗资甚巨，而且寿命极短。所以，超冷强相互作用费米气体就是开展实验研究的最佳候选。

在一个处于热力学平衡态的系统中引入一个微小的扰动，让其温度不再均匀但是变化又不剧烈，如果此时没有宏观粒子流并且可以忽略热辐射，那么热传导就是系统内热量传递的主要方式。热传导是扩散现象的一个特例，遵循扩散方程。扩散现象在生活中随处可见，比如向一杯清水中滴一滴墨水，墨滴在清水中的变化就属于扩散。波动方程虽然与扩散方程在数学形式上有几分相似，但是描述了另一类截然不同的现象——波动。湖面泛起的层层涟漪，海上翻涌的滔天巨浪，车水马龙的喧嚣嘈杂，五彩斑斓的霓虹灯光，风声雨声读书声，还有越来越离不开的无线网络……这些都是波动现象。扩散与波动不仅在经典物理中至关重要，在量子多体系统中亦是举足轻重。

墨滴的扩散和水面的波动

八十多年前，朗道在建立液氦超流的二流体模型时指出，超流中不仅存在通常所说的声波，也就是密度的波动，还存在温度的波动、同时也是熵的波动，并把这种很像声波的波动称为第二声波。对于一般的物质，比如处于常规流体相的液氦，略微不均匀的温度会导致热量以扩散的方式传播，直到系统达到平衡态；但是在处于超流相的液氦中，温度的微小不均匀性可以按照波动的形式传播。朗道关于第二声波的预言后来被实验所证实。同样是超流体，强相互作用费米超流是否依然可以用二流体模型描述？是否依然存在第二声波？第一个问题的答案并不显而易见，而第二个问题的探索之路也是充满了曲折。2005年，科学家在实验上证实了超冷强相互作用费米气体的确存在超流相[1]，但是直到2013年才首次观测到了第二声波的存在[2]。在强相互作用费米超流中直接探测温度的微小波动是一件难以企及的事，所幸的是，温度波与密度波有一定程度的耦合。然而，这种耦合毕竟是微弱的，以致于第二声波的信号极易淹没在噪声的汪洋大海里。

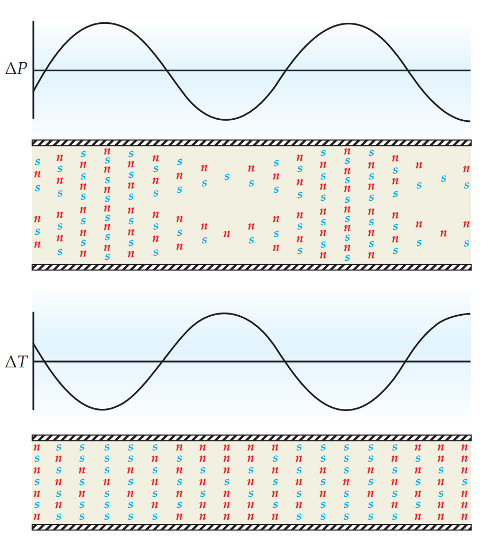
超流中的密度波动（ΔP）与温度波动（ΔT），n代表常规流体成分，s代表超流成分

（图源 Russell J. Donnelly, The two-fluid theory and second sound in liquid helium, Physics Today 62(10), 34-39, 2009）

现实中的声波在传播的过程中还会发生衰减，对于均匀介质中的平面波而言，其衰减机制可以主要归结为热量和粒子动量的扩散。热导率表征了系统内部热量的扩散，或者说热传导；粒子动量的扩散与流体的黏性息息相关，表征这一性质的物理量叫做黏滞系数，又名黏度。日常生活经验告诉我们，与水相比，油显得黏糊糊的；如果用“物理”一点的话来说，就是油的黏滞系数比水的大。既然声波的衰减与热传导以及黏滞现象都有关联，那么，对声波衰减率的测量将会提供关于系统热导率和黏滞系数的信息。

不同黏度（黏滞系数）的流体，左图中水的黏性远小于右图中蜂蜜的黏性

（图源 sciencenotes.org）

作为超流之中独一无二的存在，第二声波的传播和衰减还可以帮助我们研究超流相变的临界现象。物理上把相变分为一级相变和连续相变两类。固相与液相之间的相变、临界点以下的气相与液相之间的相变都属于一级相变，普通导体与常规超导体之间的相变、常规流体与超流体之间的相变都属于连续相变。连续相变在临界点附近存在一个临界区，标度理论认为，对于处在临界区的系统来说，发散的关联长度导致诸多热力学函数也出现了奇异性，并且这些奇异性之间的关系存在普适性。而动力学标度理论则致力于研究系统在临界区的黏性、热传导、线性响应等动力学性质，可以完善我们对连续相变临界现象的认识。但是，无论是高温超导还是液氦超流，其临界区都比较狭窄，不利于开展对其临界动力学的实验研究。所幸的是，超冷原子系统具有极佳的可控性，有望实现较宽的超流相变临界区，而对第二声波的传播和衰减的研究也将为动力学标度理论的发展提供助力。

虽然强相互作用费米超流的第二声波已经被观测到了，但是受限于当时的实验技术，系统处于平衡态时其密度是不均匀的，这就阻碍了对声波衰减的界定和定量研究[2]。近四五年来，密度均匀的强相互作用费米超流才被制备出来；近两年来，其第一声波的衰减得到了定量的研究[3]。可是，该系统的粒子数较少、费米能偏低，于是第二声波的频率就很小，对实验装置的能量分辨率便提出了极为苛刻的要求。此时，遑论其衰减，就连对第二声波本身的观测都成了困难。

中国科学技术大学潘建伟、姚星灿、陈宇翱等人组成的研究团队经过逾四年的艰苦攻关，搭建了一个全新的超冷锂-镝原子量子模拟平台，融合并发展了诸多领先的超冷原子调控手段，如灰色光学黏胶、算法冷却、三维盒型光势阱等，最终成功地实现了具有世界顶尖水平的均匀费米气体制备技术。在此基础上制备的强相互作用费米超流由约1000万个费米原子组成，费米能达到了50 kHz，相较于世界上其他研究小组的已报道结果来说均提高了约1个数量级。此外，对强相互作用费米超流的控制精度也达到了极高的水平，例如，温度的控制精度优于0.01倍费米温度，密度的非均匀性小于2%，体系加热率被抑制到了可忽略的水平，等等。在此基础上，通过一项新颖的探测手段——低动量传递（约0.05倍费米动量）与高能量分辨率（优于0.001费米能）的布拉格谱技术，系统在长波极限下的密度响应函数可以被实验直接定量观测。把领先的制备技术和探测技术相结合，研究团队成功地在强相互作用费米超流的密度响应中观测到了第二声波的信号。接着，通过改变体系温度与布拉格晶格的频率，强相互作用费米超流的密度响应谱得到了完整的、细致的测量，并且实验结果与基于耗散二流体模型的拟合曲线高度吻合。

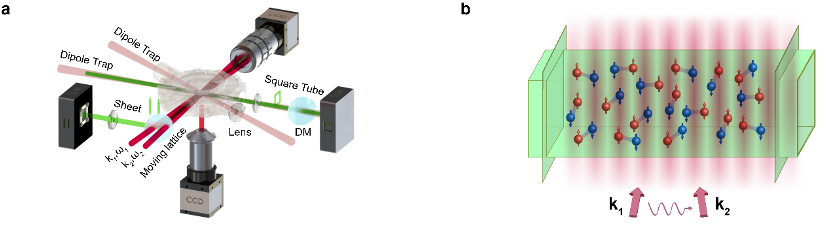
(a)实验装置示意图；(b)实验方案示意图

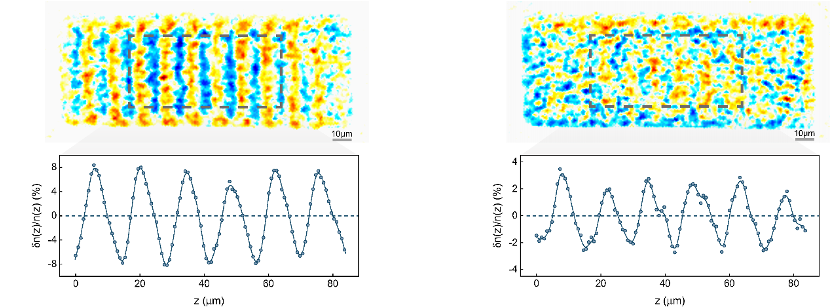
强相互作用费米超流中的第一声波（左图）与第二声波（右图）的信号

进一步地，中国科学技术大学的研究团队与斯威本科技大学的胡辉教授合作，在耗散二流体模型的基础上，不仅定量地获得了强相互作用费米超流在超流相变附近的第一、第二声波的声速及衰减率，而且验证了强相互作用费米超流的物态方程，甚至由此获得了比前人的测量结果更加精确的超流占据数（superfluid fraction）。更为重要的是，黏滞系数和热导率这两个输运参数被独立地提取出来，并且都接近于量子力学所赋予的极限。这些极限值仅由普朗克常数、玻尔兹曼常数以及粒子的密度与质量所决定，与系统的其他细节无关，是普适性的体现。此外，实验结果表明，黏滞和热传导对声波衰减的贡献是同等重要的。这些结果为我们深入研究其他形态的强相互作用费米超流（例如中子星地壳、夸克-胶子等离子体）、乃至其他强关联费米系统（例如非常规超导体）提供了重要的实验信息，因而这项工作是使用量子模拟来研究重要物理问题的一个范例。还有一个令人惊喜的收获是，在此项工作中制备的强相互作用费米超流的临界区宽度大约是液氦超流的一百倍，如此之宽的超流相变临界区与优秀的温度控制精度相配合，将为日后观测相变临界点附近的反常输运现象、测量动力学标度函数、发展动力学标度理论提供良好的基础。

（责任编辑：陈卓）

（版权说明，转载自：墨子沙龙公众号）