工欲善其事,必先利其器。

工欲善其事,必先利其器。人工智能,人类发明史上的皇冠,要完成如此伟业,自然更加需要找到足够锋利之器。而电子计算机就是迄今为止最佳的答案。
电子计算机的诞生
现今,任何一个计算器都可以秒杀人类所有算术天才,但其发展却远非一蹴而就,其中包含无数先贤的灵光闪现和辛勤努力。在古代,东方也许在这方面是领先的。中国人发明了算筹和算盘。但是这两者在复现的自动化程度上,都属于辅助工具。西方后来居上, 1642年,法国数学家帕斯卡发明了自动滚轮式加法器。1671年,莱布尼茨在其基础上发明了乘法器,基本可以实现自动四则运算。1822年,巴贝奇又进行了大幅改进,发明了差分机和分析机,奠定了现代电子计算机的基础,催生了第一台电子计算机ENIAC于1946年在美国宾夕法尼亚大学诞生【关于ENIAC和阿塔纳索夫-贝瑞计算机(Atanasoff–Berry Computer,ABC)谁才是第一台电子计算机,一直存在争议。后者虽然更早,但不是通用计算机,不是图灵完全的。因此,这里还是采用ENIAC是第一台电子计算机的说法】。




从可计算性理论角度,电子计算机实现了通用图灵机模型。通用图灵机的计算能力和递归函数等价。著名的“丘奇—图灵论题”论断:
“任何在算法上可计算的问题同样可由图灵机计算。”
很多经验和事实都间接地验证了这个论断。也就是说,从可计算性理论角度,电子计算机基本达到了机器所能达到的上限。
电子计算机在实践上的突破更为惊人。摩尔定律声称,每隔18-24个月,计算机的性能将提高一倍。第一台通用计算机ENIAC每秒能做5000次加法(已经远远超过人类手工计算),但现在的超级计算机神威·太湖之光峰值运算能力达到每秒12.5亿亿次!ENIAC重达30余吨,而现在普通电脑上用的CPU芯片才几两重,每秒能做几百上千亿次浮点运算。
由于强大的能力,计算机在方方面面、各行各业的应用也是突飞猛进,包括万维网、信息和软件系统、数据库、虚拟社交网络、智能手机、电子游戏、科学计算等等。可以说,电子计算机已经完全改变了人类的生活方式,也带来了无限可能。最近几十年内涌现的商业巨头,绝大部分都和计算机直接或间接相关,例如,微软、谷歌、亚马逊、Facebook、腾讯、阿里巴巴和百度等等。
在电子计算机诞生之前,人工智能的梦想虽然伟大和激动人心,但在相当长的一段时间内,苦于没有强大的工具支撑,人类在这方面的进展委实乏善可陈。电子计算机的诞生给人工智能带来了新的可能。
计算机与人工智能
有意思的是,电子计算机和人工智能的正式诞生几乎在同一个时期。
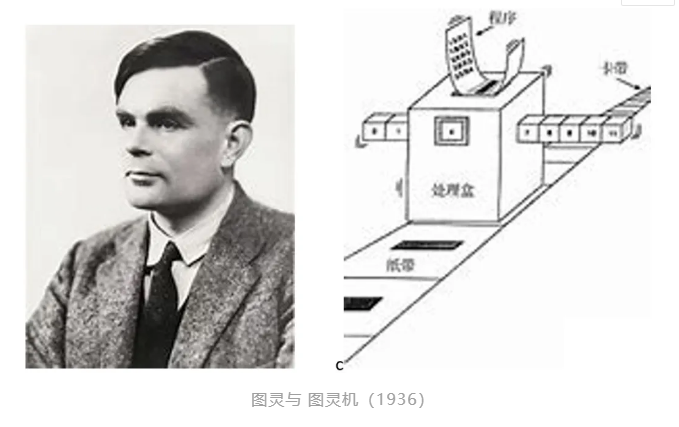
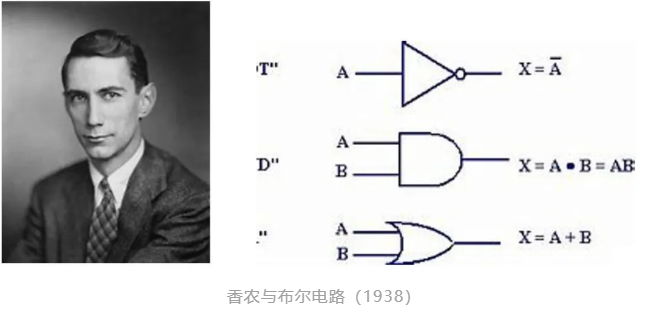
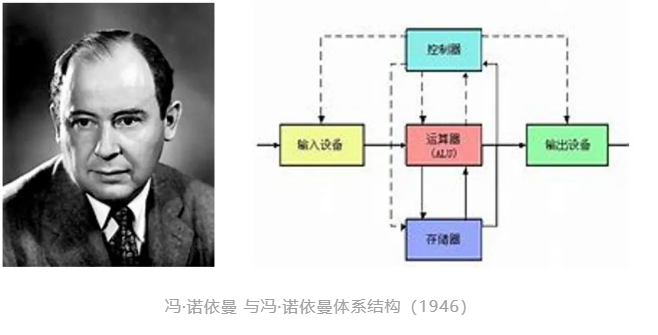
1936年,图灵提出了著名的图灵机[1],为电子计算机的实现奠定了理论基础;1938年,香农的硕士论文提出了数字布尔电路设计,指出布尔值真假可以和电路的开关相对应[2];1946年,冯·诺依曼将图灵机具象化,提出了冯·诺依曼体系结构[3],指导如何具体实现一个通用图灵机。在这些理论工作的基础上,第一台通用实体电子计算机ENIAC于1946年诞生。而第二代的基于冯·诺依曼体系结构的EDVAC诞生于1951年,这也是现代电子计算机的真正鼻祖。

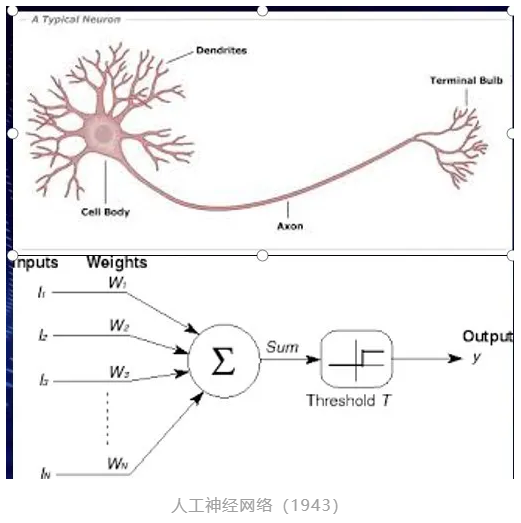
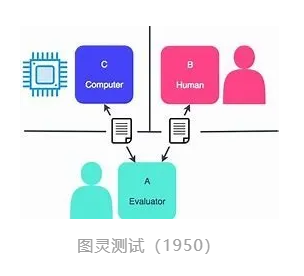
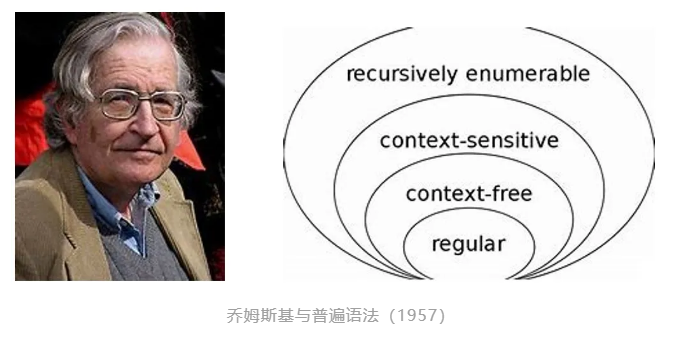
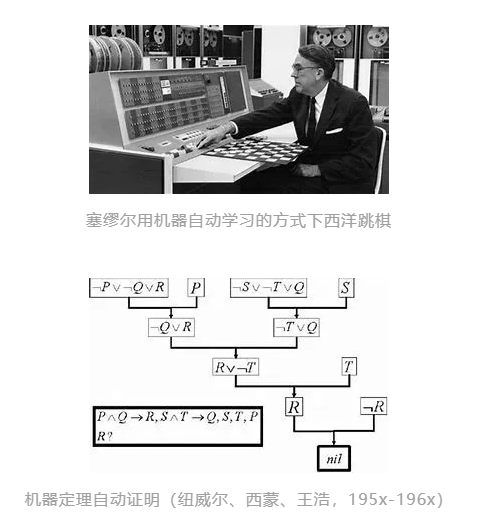
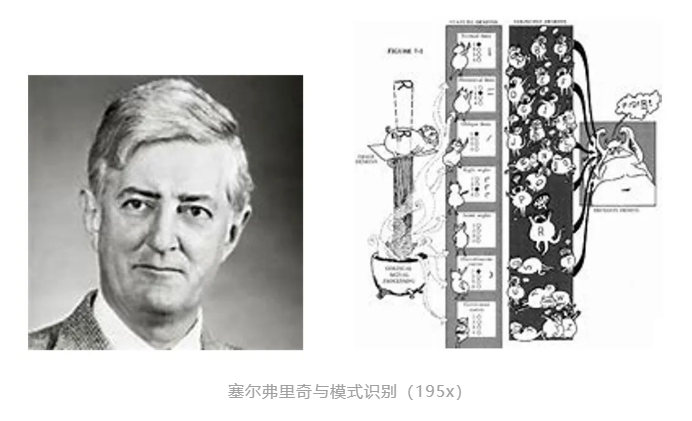
与此同时,人工智能作为一门独立的学科开始萌芽。1943年,麦卡洛克和皮茨提出了人工神经元的数学模型,并讨论了两层的神经网络和布尔电路之间的关系[4]。同样是图灵,在1950年提出了“图灵测试”[5],试图用一种可操作的方法去判断机器是否具有智能。明斯基的博士论文(1954年)系统地讨论了神经网络,并尝试用真空管实现实体神经网络模型[6]。1955年,塞尔弗里奇开展了在图像上模式识别的奠基性工作[7]。乔姆斯基于1957年提出了语言的语法结构,揭示了通用自然语言的语句如何通过少量的语法规则生成[8]。罗森布拉特于1958年提出了名为“感知机”(Perceptrons)的神经网络模型[9]。香农、西蒙、纽威尔和肖等人开始了早期对机器下国际象棋的探索[10,11]。纽威尔、西蒙以及华裔科学家王浩开展了关于机器定理自动证明的研究[12,13]。麦卡锡期望通过开发计算机编程语言LISP来表示和推理知识[14]。塞缪尔用机器自动学习的方式下西洋跳棋[15]。

达特茅斯会议开启人工智能
随着这些研究所推动的新思潮,人工智能也自然而然应运而生。一般认为,1956年举办的达特茅斯会议“人工智能暑期研究计划”(“Summer Research Project on Artificial Intelligence”)是人工智能正式诞生的标志。但事实上,在同时期,还有其他会议也对人工智能的诞生非常重要,包括1955年的一次关于机器学习和模式识别的会议“学习机器会议”(“Session on Learning Machines”),以及1958年的一次关于机器是否能够思考的讨论“思考过程的机械化”。有意思的是,在1955年的会议中,就出现了人工智能中两个大的流派,即符号流派和联接流派的争端。其中纽威尔代表符号学派,而塞尔弗里奇代表联接流派。将来,我们将着重讨论这一点。

之所以达特茅斯会议被公认为人工智能诞生的标志,主要有以下几方面的原因。第一,达特茅斯会议首次使用了“人工智能”(Artificial Intelligence)一词,虽然该词当时并不被所有与会者认同。第二,达特茅斯会议中很多重要的参与者,都成了人工智能的先驱人物,包括麦卡锡、明斯基、纽威尔和西蒙,而这四人通常被认为是“人工智能之父”。再者,达特茅斯会议提出了很多重要的工作和思想,包括纽威尔和西蒙的“逻辑理论家”(Logic theorist)等。而1958年的会议有了更多成熟的思想和工作,其中包括明斯基关于启发式编程的论文,麦卡锡关于“常识知识”(Commonsense knowledge)的初步探索,以及塞尔弗里奇关于模式识别的“群魔殿”(Pandemonium)工作,等等。
至此,我,人工智能,跟随着孪生哥哥电子计算的脚步,正式诞生了。

(责任编辑:屠津伟)
(版权说明,转载自:墨子沙龙公众号)

参考文献:
[1] A. M. Turing, On Computable Numbers, with an Application to the
Entscheidungs problem, Proceedings of the London Mathematical Society, Series 2, Vol. 42, pp. 230-265, 1936.
[2] C. Shannon. A Symbolic Analysis of Relay and Switching Circuits. Master thesis. 1938.
[3]J. Von Neuman. First Draft of a Report on the EDVAC. 1946.
[4] W.S. McCulloch, W. Pitts. A logical calculus of the ideas immanent in nervous activity. The bulletin of mathematical biophysics, 5(4):115-133, 1943.
[5] A. M. Turing, Computing Machinery and Intelligence, Mind, Vol. LIX, No. 236, pp. 433-460, 1950.
[6] M. L. Minsky. Theory of Neural-Analog Reinforcement Systems and Its Application to the Brain-Model Problem, Ph.D. thesis, Princeton University, 1954.
[7] O. Selfridge, Pattern Recognition and Modern Computers, In Proceedings of the 1955 Western Joint Computer Conference, Institute of Radio Engineers, New York, pp. 91-93,1955.
[8] N. Chomsky, Syntactic Structures. Mouton & Co.'s-Gravenhage, 1957.
[9] F. Rosenblatt, The Perceptron: A Probabilistic Model for Information Storage and Organization in the Brain. Psychological Review, Vol. 65, pp.386, 1958.
[10] C. Shannon, Programming a Computer for Playing Chess, Philosophical Magazine, Ser. 7, Vol. 41, No. 314, 1950.
[11] A. Newell, J. Shaw, and H.A. Simon, Chess-Playing Programs and the Problem of Complexity. IBM Journal of Research and Development, Vol. 2, pp. 320-335, 1958.
[12] A. Newell and H. A. Simon, The Logic Theory Machine: A Complex Information Processing System. Proceedings IRE Transactions on Information Theory, Vol. IT-2, pp. 61-79, 1956.
[13] H. Wang. Proving Theorems by Pattern Recognition. Communications of the ACM, Vol. 4, No. 3, pp. 229-243, 1960.
[14] J. McCarthy:Recursive Functions of Symbolic Expressions and Their Computation by Machine, Part I. Communication of the ACM 3(4): 184-195, 1960.
[15] A. L. Samuel, Some Studies in Machine Learning Using the Game of Checkers,"IBM Journal of Research and Development, Vol. 3, No. 3, pp. 210-229, 1959.
